题目内容
11.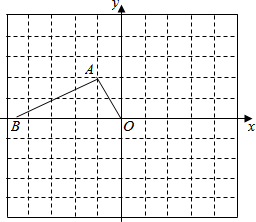 如图,在Rt△AOB中,∠A=90°,∠AOB=60°,在边长为1的小正方形组成的网格中,△AOB的顶点O、A均在格点上,点B在x轴上,点A的坐标为(-1,2).
如图,在Rt△AOB中,∠A=90°,∠AOB=60°,在边长为1的小正方形组成的网格中,△AOB的顶点O、A均在格点上,点B在x轴上,点A的坐标为(-1,2).(1)点A关于点O中心对称的点的坐标为(1,-2);
(2)△AOB绕点O顺时针旋转60°后得到△A1OB1,那么点A1的坐标为(1,2);线段AB在旋转过程中所扫过的面积是$\frac{5π}{2}$.
分析 (1)根据关于原点对称的点的坐标特点,即可得出答案;
(2)由旋转的性质可求得点A1的坐标,线段AB扫过的面积=${S}_{扇BO{B}_{1}}-{S}_{△AOB}+{S}_{△{A}_{A}{B}_{1}0}-{S}_{扇AO{A}_{1}}$=${S}_{扇BO{B}_{1}}-{S}_{扇AO{A}_{1}}$从而可求得答案.
解答 解:(1)∵点A的坐标为(-1,2),
∴A关于点O中心对称的点的坐标为(1,-2);
(2)如图所示: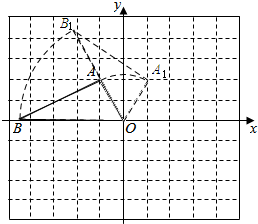
根据图形可知:点A1的坐标为(1,2).
由点A的坐标可知:OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵∠AOB=60°,
∴∠AOB=30°.
∴OB=2OA=2$\sqrt{5}$.
由旋转的性质可知:${S}_{△ABO}={S}_{△{A}_{1}{B}_{1}O}$.
线段AB扫过的面积=${S}_{扇BO{B}_{1}}-{S}_{△AOB}+{S}_{△{A}_{A}{B}_{1}0}-{S}_{扇AO{A}_{1}}$=${S}_{扇BO{B}_{1}}-{S}_{扇AO{A}_{1}}$=$\frac{60°π×(2\sqrt{5})^{2}}{360°}$-$\frac{60°π×(\sqrt{5})^{2}}{360°}$=$\frac{5π}{2}$.
故答案为:(1)(1,-2);(2)(1,2);$\frac{5π}{2}$.
点评 本题考查了利用旋转变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在画二次函数的图象时列出了下表:
观察表格,可以得到许多信息:
(1)抛物线的对称轴是直线x=1;当x=-2时,对应的y值是-5;
(2)我们还发现,在对称轴右侧,当x每增加1个单位时,对应y值除了趋势逐渐变小外,在数量上还存在某种规律,试利用这一规律,直接写出当x=5时,对应的y值是-12;
(3)函数y=ax2+bx+c(a、b、c为常数,a≠0)图象上有三点:A(m,y1)、B(m+1,y2)、C(m+2,y3).通过计算说明:(y3-y2)与(y2-y1)的差为定值.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 0 | 3 | 4 | 3 | 0 | -5 | … |
(1)抛物线的对称轴是直线x=1;当x=-2时,对应的y值是-5;
(2)我们还发现,在对称轴右侧,当x每增加1个单位时,对应y值除了趋势逐渐变小外,在数量上还存在某种规律,试利用这一规律,直接写出当x=5时,对应的y值是-12;
(3)函数y=ax2+bx+c(a、b、c为常数,a≠0)图象上有三点:A(m,y1)、B(m+1,y2)、C(m+2,y3).通过计算说明:(y3-y2)与(y2-y1)的差为定值.
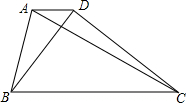 如图,在梯形ABCD中,AD∥BC,已知AD=2,BD=6,AC=BC=8,求证:AC⊥BD.
如图,在梯形ABCD中,AD∥BC,已知AD=2,BD=6,AC=BC=8,求证:AC⊥BD.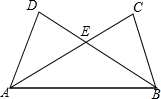 已知,如图,AD=BC,AC=BD,AC与BD相交于点E.
已知,如图,AD=BC,AC=BD,AC与BD相交于点E.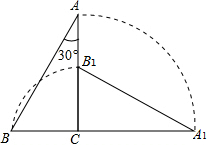 如图,把一个斜边长为4且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的面积是$\frac{11}{3}$π+$\sqrt{3}$.
如图,把一个斜边长为4且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的面积是$\frac{11}{3}$π+$\sqrt{3}$. 如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.
如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.
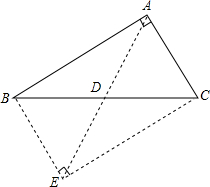 已知,如图所示,△ABC是直角三角形,∠BAC=90°,AD是BC边上的中线,求证:AD=BD=CD.
已知,如图所示,△ABC是直角三角形,∠BAC=90°,AD是BC边上的中线,求证:AD=BD=CD.