题目内容
9.如图,有一座抛物线形拱桥,当桥拱顶点距水面6m高时,桥下水面宽AB=20m.随着水位的上升,桥下水面的宽度逐渐减小,当水位上升到水面宽为10m(即CD位置)时,就达到了警戒线.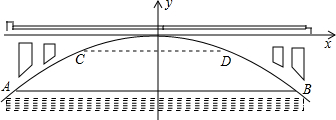
(1)在如图的直角坐标系中,求抛物线的函数表达式.
(2)当洪水来临时,水位以每小时0.2m的速度上升,多少时间后水位达到警戒线?
分析 (1)首先设所求抛物线的解析式为:y=ax2(a≠0),再根据题意得到A(-10,-6),利用待定系数法即可得到抛物线解析式;
(2)根据抛物线解析式计算出C点坐标,进而得到F点坐标,然后计算出EF的长,再算出持续时间即可.
解答 解:(1)设所求抛物线的解析式为:y=ax2(a≠0),
∵由AB=20m,桥拱顶点距水面6m,
则A(-10,-6),
把A的坐标分别代入y=ax2得:-6=100a,
解得:a=-$\frac{3}{50}$.
故抛物线的函数表达式为:y=-$\frac{3}{50}$x2;
(2)∵DC宽10m,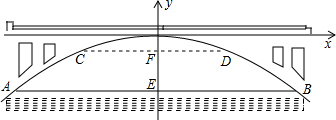
∴设C(-5,b),
把C点坐标代入抛物线的解析式为y=-$\frac{3}{50}$x2中,
解得:b=-$\frac{3}{2}$,
∴F(0,-$\frac{3}{2}$),
∴EF=6-$\frac{3}{2}$=4.5(m),
∵水位以每小时0.2m的速度上升,
∴4.5÷0.2=22.5(小时).
答:从正常水位开始,持续22.5小时到达警戒线.
点评 此题主要考查了二次函数的应用,关键是正确得到C点坐标,求出抛物线解析式.

练习册系列答案
相关题目
4.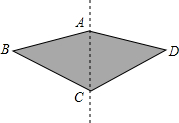 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
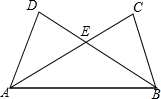 已知,如图,AD=BC,AC=BD,AC与BD相交于点E.
已知,如图,AD=BC,AC=BD,AC与BD相交于点E.
 如图,△ABC中,D为AB的中点,AD=5厘米,∠B=∠C,BC=8厘米.
如图,△ABC中,D为AB的中点,AD=5厘米,∠B=∠C,BC=8厘米. 如图,四边形ABCD内接于⊙O,点E是BC延长线上一点,连接OB、OD,∠DCE=55°,则∠BOD=110°.
如图,四边形ABCD内接于⊙O,点E是BC延长线上一点,连接OB、OD,∠DCE=55°,则∠BOD=110°.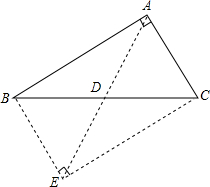 已知,如图所示,△ABC是直角三角形,∠BAC=90°,AD是BC边上的中线,求证:AD=BD=CD.
已知,如图所示,△ABC是直角三角形,∠BAC=90°,AD是BC边上的中线,求证:AD=BD=CD.