题目内容
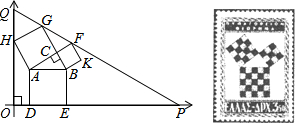
10. 已知,如图,在四边形ABCD中,AC=BD,且相交于点O,E,F为AB,CD的中点,EF分别交AC,BD于点G,H,求证:OG=OH.
已知,如图,在四边形ABCD中,AC=BD,且相交于点O,E,F为AB,CD的中点,EF分别交AC,BD于点G,H,求证:OG=OH.
分析 取BC边的中点M,连接EM,FM,则根据三角形的中位线定理,即可证得△EMF是等腰三角形,根据等边对等角,即可证得∠MEF=∠MFE,然后根据平行线的性质证得∠OGH=∠OHG,根据等角对等边即可证得.
解答 解:取BC边的中点M,连接EM,FM,
∵M、F分别是BC、CD的中点,
∴MF∥BD,MF=$\frac{1}{2}$BD,
同理:ME∥AC,ME=$\frac{1}{2}$AC,
∵AC=BD,
∴ME=MF,
∴∠MEF=∠MFE,
∵MF∥BD,
∴∠MFE=∠OGH,
同理∠MEF=∠OHG,
∴∠OGH=∠OHG,
∴OG=OH.
点评 本题考查了三角形的中位线定理,正确证明△EMF是等腰三角形是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
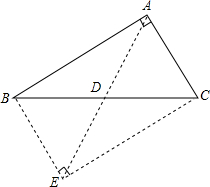 已知,如图所示,△ABC是直角三角形,∠BAC=90°,AD是BC边上的中线,求证:AD=BD=CD.
已知,如图所示,△ABC是直角三角形,∠BAC=90°,AD是BC边上的中线,求证:AD=BD=CD. 如图,A,B,C是同一直线上的三个点,图中共有几条射线?在不增加字母的情况下,能表示出的射线共几条?是哪几条?
如图,A,B,C是同一直线上的三个点,图中共有几条射线?在不增加字母的情况下,能表示出的射线共几条?是哪几条?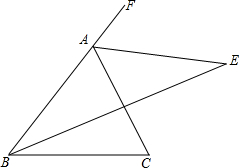 如图,在△ABC中,∠B的平分线与∠BAC的外角平分线相交于点E.
如图,在△ABC中,∠B的平分线与∠BAC的外角平分线相交于点E.