题目内容
19.不等式组$\left\{\begin{array}{l}{2x-8<0}\\{1+x>0}\end{array}\right.$的解集是-1<x<4.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式2x-8<0,得:x<4,
解不等式1+x>0,得:x>-1,
∴不等式组的解集为-1<x<4,
故答案为:-1<x<4.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
9.已知a为实数,则下列式子一定有意义的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{a+3}$ | C. | $\frac{1}{a-1}$ | D. | $\frac{1}{\sqrt{a}}$ |
4. 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=100°,则∠2等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=100°,则∠2等于( )
 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=100°,则∠2等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=100°,则∠2等于( )| A. | 60° | B. | 50° | C. | 70° | D. | 80° |
11.已知a.b,C是三角形的三边,那么代数式a2-2ab+b2-c2的值( )
| A. | 小于零 | B. | 等于零 | C. | 大于零 | D. | 不能确定 |
8.若a-b=8,a2+b2=84,则3ab的值为( )
| A. | -30 | B. | -20 | C. | 20 | D. | 30 |
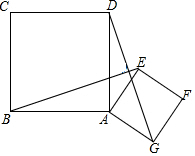 如图,已知正方形ABCD和正方形AEFG,连结BE、DG.
如图,已知正方形ABCD和正方形AEFG,连结BE、DG. 为了支援地震灾区同学,某校开展捐书活动,九(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5-4.5组别的频率是0.3,那么捐书数量在4.5-5.5组别的人数是16.
为了支援地震灾区同学,某校开展捐书活动,九(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5-4.5组别的频率是0.3,那么捐书数量在4.5-5.5组别的人数是16.