题目内容
14.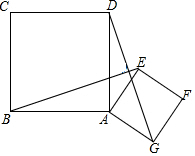 如图,已知正方形ABCD和正方形AEFG,连结BE、DG.
如图,已知正方形ABCD和正方形AEFG,连结BE、DG.(1)请你判断线段BE和DG的关系并证明你的结论;
(2)连接BD、EG、DE,点M、N、P分别是BD、EG、DE的中点,连接MP,PN,MN,请你画出图形并判断△MPN的形状,说明理由.
分析 (1)根据SAS证明△BEA与△DAG全等,再利用全等三角形的性质证明即可;
(2)由三角形中位线定理得出PM=PN,∠MPN=∠BOD=90°,即可得出结论.
解答  解:(1)BE和DG的关系是:BE=DG;BE⊥DG;理由如下:
解:(1)BE和DG的关系是:BE=DG;BE⊥DG;理由如下:
∵四边形ABCD和四边形AEFG是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAD+∠DAE=∠EAG+∠DAE,
∴∠BAE=∠DAG,
∵在△BEA与△DAG中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAE=∠DAG}&{\;}\\{AE=AG}&{\;}\end{array}\right.$,
∴△BEA≌△DAG(SAS);
∴BE=DG,∠ADG=∠ABE,
∴∠BOD=∠BAD=90°,
∴BE⊥DG;
(2)△MPN是等腰直角三角形;理由如下:
如图,由三角形中位线定理可得:MP∥BE,MP=$\frac{1}{2}$BE,PN∥DG,PN=$\frac{1}{2}$DG,
∴PM=PN,∠MPN=∠BOD=90°,
即△MPN是等腰直角三角形.
点评 此题考查了正方形的性质,三角形全等的判定与性质,三角形的中位线定理等知识;熟练掌握正方形的性质和三角形中位线定理,证明三角形全等是解决问题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
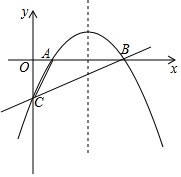 如图,抛物线y=ax2+bx-2经过点A(1,0)和点B(4,0),与y轴交于点C.
如图,抛物线y=ax2+bx-2经过点A(1,0)和点B(4,0),与y轴交于点C.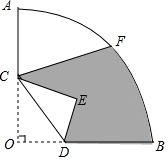 如图,在圆心角为90°的扇形AOB中,半径OA=3,OC=AC,OD=$\frac{1}{2}$BD,F是弧AB的中点.将△OCD沿CD折叠,点O落在点E处,则图中阴影部分的面积为$\frac{9π+9\sqrt{2}-12}{8}$.
如图,在圆心角为90°的扇形AOB中,半径OA=3,OC=AC,OD=$\frac{1}{2}$BD,F是弧AB的中点.将△OCD沿CD折叠,点O落在点E处,则图中阴影部分的面积为$\frac{9π+9\sqrt{2}-12}{8}$.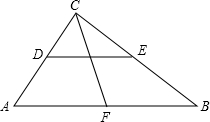 如图,在Rt△ABC中,∠ACB=90°,点F是AB的中点,CF=8cm,则中位线DE=8cm.
如图,在Rt△ABC中,∠ACB=90°,点F是AB的中点,CF=8cm,则中位线DE=8cm.