题目内容
8.(1)计算:(3-π)0-$\sqrt{8}$+|1-$\sqrt{2}$|(2)解方程:(x+3)2=(1-2x)2.
分析 (1)利用零指数幂和绝对值的意义得到原式=1-2$\sqrt{2}$+$\sqrt{2}$-1,然后合并即可;
(2)先移项得到(x+3)2-(1-2x)2=0,然后利用因式分解法解方程.
解答 解:(1)原式=1-2$\sqrt{2}$+$\sqrt{2}$-1
=-$\sqrt{2}$;
(2)(x+3)2-(1-2x)2=0,
(x+3+1-2x)(x+3-1+2x)=0,
x+3+1-2x=0或x+3-1+2x=0,
所以x1=4,x2=-$\frac{2}{3}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了实数的运算.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
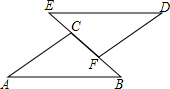 如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=8.
如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=8. 如图,正方形网格中每个小正方形的边长为1,
如图,正方形网格中每个小正方形的边长为1,