题目内容
10.已知二次函数y=ax2+bx+c的图象与x轴交于A(1,0),B(3,0)两点,与 y轴交于点C(0,3),求二次函数的顶点坐标.分析 先利用待定系数法求二次函数的解析式,再根据配方法求顶点坐标.
解答 解:把A(1,0),B(3,0),C(0,3)代入y=ax2+bx+c中得:$\left\{\begin{array}{l}{a+b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$,
∴二次函数的解析式为:y=x2-4x+3,
y=x2-4x+3=(x-2)2-1,
顶点坐标为(2,-1).
点评 本题是抛物线与x轴的交点问题,考查了利用待定系数法求二次函数的解析式,根据配方法求顶点坐标,也可以利用公式求顶点坐标:(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$).

练习册系列答案
相关题目
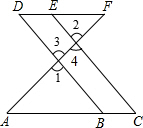 填空:如图,E点为DF上的点,B为AC上的点,已知∠1=∠2,∠C=∠D,说明DF∥AC的理由.
填空:如图,E点为DF上的点,B为AC上的点,已知∠1=∠2,∠C=∠D,说明DF∥AC的理由. 已知:如图,点E是线段AB的中点,∠A=∠B,∠AED=∠BEC.求证:CE=DE.
已知:如图,点E是线段AB的中点,∠A=∠B,∠AED=∠BEC.求证:CE=DE.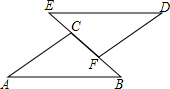 如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=8.
如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=8.