题目内容
已知x2+2x+y2-10y+26=0.
(1)求x+2y的平方根;
(2)求2y+2x的立方根.
(1)求x+2y的平方根;
(2)求2y+2x的立方根.
考点:配方法的应用,非负数的性质:偶次方,平方根,立方根
专题:计算题
分析:先利用配方法得到(x+1)2+(y-5)2=0,则根据非负数的性质得到x+1=0,y-5=0,解得x=-1,y=5,
(1)先计算x+2y的值,然后根据平方根的定义求解;
(2)先计算2y+2x的值,然后根据立方根的定义求解.
(1)先计算x+2y的值,然后根据平方根的定义求解;
(2)先计算2y+2x的值,然后根据立方根的定义求解.
解答:解:∵x2+2x+y2-10y+26=0,
∴x2+2x+1+y2-10y+25=0,
∴(x+1)2+(y-5)2=0,
∴x+1=0,y-5=0,
∴x=-1,y=5,
(1)x+2y=-1+2×5=9,所以x+2y的平方根为±
=±3;
(2)2y+2x=2×5+2×(-1)=8,所以2y+2x的立方根为
=2.
∴x2+2x+1+y2-10y+25=0,
∴(x+1)2+(y-5)2=0,
∴x+1=0,y-5=0,
∴x=-1,y=5,
(1)x+2y=-1+2×5=9,所以x+2y的平方根为±
| 9 |
(2)2y+2x=2×5+2×(-1)=8,所以2y+2x的立方根为
| 3 | 8 |
点评:本题考查了配方法的应用:用配方法解一元二次方程;利用配方法求二次三项式是一个完全平方式时所含字母系数的值.也考查了非负数的性质.

练习册系列答案
相关题目
如果x>y>0,那么
-
的值是( )
| y+1 |
| x+1 |
| y |
| x |
| A、零 | B、正数 | C、负数 | D、无法确定 |
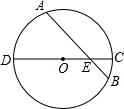 如图,CD为⊙O的直径,弦AB交CD于点E,∠CEB=45°,DE=9cm,CE=3cm,求弦AB的长.
如图,CD为⊙O的直径,弦AB交CD于点E,∠CEB=45°,DE=9cm,CE=3cm,求弦AB的长.