题目内容
求二次函数y=mx2+2mx+3（m＞0）的图象的对称轴，并说出该函数具有哪些性质？
考点：二次函数的性质
专题：
分析：利用二次函数的对称轴公式x=-
，代入可求得其对称轴，再根据m＞0说出其性质即可．
| b |
| 2a |
解答：解：
其对称轴为x=-
=-1，且m＞0，
所以该二次函数开口向上，当x=-1时，有最小值3-m，当x＜-1时，y随x的增大而减小，当x＞-1时，y随x的增大而增大．
其对称轴为x=-
| 2m |
| 2m |
所以该二次函数开口向上，当x=-1时，有最小值3-m，当x＜-1时，y随x的增大而减小，当x＞-1时，y随x的增大而增大．
点评：本题主要考查二次函数的对称轴及二次函数的性质，掌握二次函数的对称轴公式及二次函数的增减性是解题的关键．
练习册系列答案
字词句段篇系列答案
相关题目
已知一组数据的平均数为
，若在这组数据中再添加一个数
，则所得新数据的方差与原数据的方差相比较（ ）
. |
| x |
. |
| x |
| A、变大 | B、变小 |
| C、相等 | D、无法确定 |
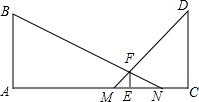如图所示，晚上小亮走在大街上，他发现当他站在大街上高度相等的两盏路灯AB和CD之间时，自己右边的影子NE的长为3m，左边的影子ME的长为1.5m，又知小亮的身高EF为1.80m，两盏路灯AC之间的距离为12m，点A、M、E、N、C在同一条直线上，问：路灯的高为多少米？