题目内容
13. 如图,把△ABC沿着AB方向平移到△A1B1C1的位置时,它们重叠部分的面积是△A1B1C1面积的一半,若AB=4,平移的距离2$\sqrt{2}$.
如图,把△ABC沿着AB方向平移到△A1B1C1的位置时,它们重叠部分的面积是△A1B1C1面积的一半,若AB=4,平移的距离2$\sqrt{2}$.
分析 利用重叠面积为△A1B1C1面积的一半,得出相似比,进而求出A1B的长.
解答 解:∵重叠部分的面积是△A1B1C1面积的一半,
∴$\frac{{A}_{1}B}{{A}_{1}{B}_{1}}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∵AB=A1B1=4,
∴A1B=2$\sqrt{2}$,
∴平移的距离为:2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 此题主要考查了平移的性质,正确利用相似三角形的性质得出A1B的长是解题关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
1.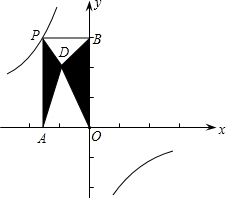 如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )
如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )
 如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )
如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )| A. | y=-$\frac{5}{x}$ | B. | y=-$\frac{8}{x}$ | C. | y=-$\frac{10}{x}$ | D. | y=-$\frac{12}{x}$ |
18. 如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
 如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.| A. | 25.3 | B. | 26.3 | C. | 27.3 | D. | 28.3 |
 关于x的不等式x-2a≤-3的解集如图所示,则a的值是1.
关于x的不等式x-2a≤-3的解集如图所示,则a的值是1. AB是圆O的直径,点C,D都在圆O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AC的长是3$\sqrt{3}$.
AB是圆O的直径,点C,D都在圆O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AC的长是3$\sqrt{3}$.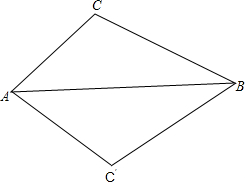 如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA.
如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA. 如图所示,DE∥BC,∠1=∠2,求证:EF∥AB.
如图所示,DE∥BC,∠1=∠2,求证:EF∥AB.