题目内容
15.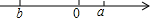 已知实数,在数轴上的位置如图所示,则以下三个命题:①a3-ab2<0,②$\sqrt{{{(a+b)}^2}}=a+b$,③$\frac{1}{a+b}<\frac{1}{a}$,其中真命题的序号为①.
已知实数,在数轴上的位置如图所示,则以下三个命题:①a3-ab2<0,②$\sqrt{{{(a+b)}^2}}=a+b$,③$\frac{1}{a+b}<\frac{1}{a}$,其中真命题的序号为①.
分析 先由数轴上a,b两点的位置,判断出a,b的符号及绝对值的大小,再分别代入各式计算即可解决问题.
解答 解:由实数a、b在数轴上的位置得b<0<a,|b|>|a|,
那么a3-ab2=a(a2-b2),a>0,a2-b2<0,故a3-ab2<0,故①正确;
$\sqrt{(a+b)^{2}}$=-a-b,故②错误;
$\frac{1}{a+b}$中分母为负数,$\frac{1}{a+b}$<0,因a>0,$\frac{1}{a}$>0,故$\frac{1}{a+b}$<$\frac{1}{a}$,故③错误.
故答案为:①.
点评 此题主要考查了实数与数轴之间的对应关系及绝对值的化简,主要利用数轴考查不等式与等式是否成立.考查的知识点为:绝对值大的数的平方也大;负数的绝对值是它的相反数.

练习册系列答案
相关题目
20.九边形的外角和是( )
| A. | 1 620度 | B. | 1 440度 | C. | 720度 | D. | 360度 |
 如图,O是直线AB上的任一点,且OC⊥OD,∠1=35°,则∠2=55度.
如图,O是直线AB上的任一点,且OC⊥OD,∠1=35°,则∠2=55度. 如图,将△OAB绕点O按逆时针方向旋转至△OA′B′,这时点B在边A′B′上,已知AB=5cm,BB′=2cm,则A′B的长是3cm.
如图,将△OAB绕点O按逆时针方向旋转至△OA′B′,这时点B在边A′B′上,已知AB=5cm,BB′=2cm,则A′B的长是3cm. 关于x的不等式x-2a≤-3的解集如图所示,则a的值是1.
关于x的不等式x-2a≤-3的解集如图所示,则a的值是1. 某校数学兴趣小组用高为1.5米的仪器测量建筑物CD的高度,如图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α,测得A、B之间的距离为2米,tanα=$\frac{6}{5}$,tanβ=$\frac{10}{9}$,试求建筑物CD的高度.
某校数学兴趣小组用高为1.5米的仪器测量建筑物CD的高度,如图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α,测得A、B之间的距离为2米,tanα=$\frac{6}{5}$,tanβ=$\frac{10}{9}$,试求建筑物CD的高度.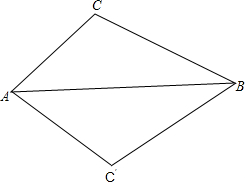 如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA.
如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA.