题目内容
9. 如图,在△ABC中,已知∠A=50°,OB、OC平分∠ABC和∠ACB,则∠BOC的度数是( )
如图,在△ABC中,已知∠A=50°,OB、OC平分∠ABC和∠ACB,则∠BOC的度数是( )| A. | 72° | B. | 54° | C. | 46° | D. | 115° |
分析 由三角形内角和定理求出∠ABC+∠ACB=180°-∠A=130°,由角平分线的定义得出∠OBC+∠OCB=65°,再由三角形内角和定理即可求出∠BOC的度数.
解答 解:∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,
∵OB、OC分别平分∠ABC、∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°;
故选:D.
点评 本题考查了三角形内角和定理、角平分线的定义;熟练掌握三角形内角和定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
19. 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )| A. | SSS | B. | AAS | C. | SAS | D. | HL |
20.九边形的外角和是( )
| A. | 1 620度 | B. | 1 440度 | C. | 720度 | D. | 360度 |
17.等腰三角形的一个角是50°,则它顶角的度数是( )
| A. | 80°或50° | B. | 80° | C. | 80°或65° | D. | 65° |
14.已知反比例函数y=-$\frac{2}{x}$,下列结论不正确的是( )
| A. | y随x的增大而增大 | B. | 图象必经过点(-1,2) | ||
| C. | 图象在第二、四象限内 | D. | 若x>1,则-2<y<0 |
1.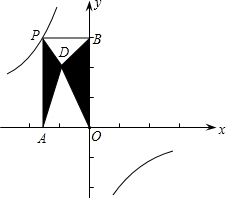 如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )
如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )
 如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )
如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )| A. | y=-$\frac{5}{x}$ | B. | y=-$\frac{8}{x}$ | C. | y=-$\frac{10}{x}$ | D. | y=-$\frac{12}{x}$ |
18. 如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
 如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.
如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD(精确到0.1m)是( )m.| A. | 25.3 | B. | 26.3 | C. | 27.3 | D. | 28.3 |
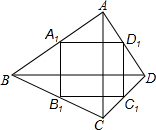 如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1是四边形ABCD对应边上的中点.如果AC=8,BD=10,那么四边形A1B1C1D1周长为18.
如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1是四边形ABCD对应边上的中点.如果AC=8,BD=10,那么四边形A1B1C1D1周长为18.