题目内容
7.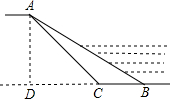 为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少?
为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少?
分析 分别在Rt△ABD和Rt△ACD中求出AD、BD、CD的长度,然后求出BC的长度,求出△ABC的面积,最后求出需清理的土方量.
解答 解:在Rt△ABD中,
∵AB=12m,AD:BD=1:$\sqrt{3}$,
∴AD=6m,BD=6$\sqrt{3}$m,
在Rt△ACD中,
∵∠ACD=45°,
∴CD=AD=6m,
∴BC=6$\sqrt{3}$-6(m),
则S△ABC=$\frac{1}{2}$×6×(6$\sqrt{3}$-6)=18($\sqrt{3}$-1)(m2)
则土方量为:18($\sqrt{3}$-1)×800=14400($\sqrt{3}$-1)m3.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据坡度和坡角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
相关题目
12.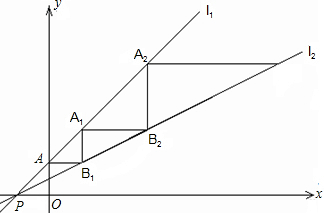 如图,直线l1:y=x+1与直线l2:y=$\frac{1}{2}$x+$\frac{1}{2}$相交于点P(-1,0),直线l1与y轴交于点A,一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B2处后,改为垂直于x轴的方向运动,到达直线l1上的A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,达到直线l1上的点A2处后,仍沿平行于x轴的方向运动,…照此规律运动,动点C依次经过点B1,A1,B2,A2,B3,A3,…,B2015,A2015,…则当动点C到达A2015处时,运动的总路径的长为( )
如图,直线l1:y=x+1与直线l2:y=$\frac{1}{2}$x+$\frac{1}{2}$相交于点P(-1,0),直线l1与y轴交于点A,一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B2处后,改为垂直于x轴的方向运动,到达直线l1上的A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,达到直线l1上的点A2处后,仍沿平行于x轴的方向运动,…照此规律运动,动点C依次经过点B1,A1,B2,A2,B3,A3,…,B2015,A2015,…则当动点C到达A2015处时,运动的总路径的长为( )
 如图,直线l1:y=x+1与直线l2:y=$\frac{1}{2}$x+$\frac{1}{2}$相交于点P(-1,0),直线l1与y轴交于点A,一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B2处后,改为垂直于x轴的方向运动,到达直线l1上的A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,达到直线l1上的点A2处后,仍沿平行于x轴的方向运动,…照此规律运动,动点C依次经过点B1,A1,B2,A2,B3,A3,…,B2015,A2015,…则当动点C到达A2015处时,运动的总路径的长为( )
如图,直线l1:y=x+1与直线l2:y=$\frac{1}{2}$x+$\frac{1}{2}$相交于点P(-1,0),直线l1与y轴交于点A,一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B2处后,改为垂直于x轴的方向运动,到达直线l1上的A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,达到直线l1上的点A2处后,仍沿平行于x轴的方向运动,…照此规律运动,动点C依次经过点B1,A1,B2,A2,B3,A3,…,B2015,A2015,…则当动点C到达A2015处时,运动的总路径的长为( )| A. | 22015-2 | B. | 22014-1 | C. | 22016-2 | D. | 22017-2 |
16.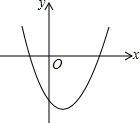 二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
 二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )| A. | 函数图象与y轴的交点坐标是(0,-3) | |
| B. | 顶点坐标是(1,-3) | |
| C. | 函数图象与x轴的交点坐标是(3,0)、(-1,0) | |
| D. | 当x<0时,y随x的增大而减小 |
 如图,在△ABC中,∠ACB=90°,AB=5,AC=4,过点C作直线MC使得∠BCM=∠BAC,求点B到直线MC的距离.
如图,在△ABC中,∠ACB=90°,AB=5,AC=4,过点C作直线MC使得∠BCM=∠BAC,求点B到直线MC的距离.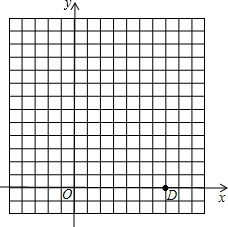 如图在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).
如图在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).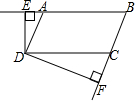 如图,在?ABCD中,DE⊥AB,DF⊥BC,∠EDF=120°,求∠B与∠BAD的度数.
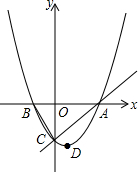
如图,在?ABCD中,DE⊥AB,DF⊥BC,∠EDF=120°,求∠B与∠BAD的度数.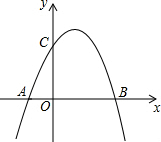 如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0),B(2,0),交y轴于C(0,2),作直线BC.
如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0),B(2,0),交y轴于C(0,2),作直线BC.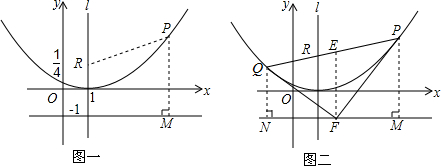
 如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.