题目内容
17.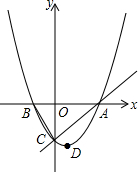 如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.(l)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围;
(3)当P点的横坐标m<0时,过P点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
分析 (1)根据函数值相等的点关于对称轴对称,可得B点坐标,根据待定系数法,可得函数解析式;
(2)根据等腰直角三角形的性质,可得射线AC、AM,根据角越小角的对边越小,可得PA在在射线AC与AM之间,根据解方程组,可得E点的横坐标,根据E、C点的横坐标,可得答案;
(3)根据相似三角形的判定与性质,可得$\frac{PQ}{CO}$=$\frac{OQ}{OB}$,根据解方程组,可得P点坐标.
解答 解:(1)由A、B点的函数值相等,得
A、B关于对称轴对称.
A(4-0),对称轴是x=1,得
B(-2,0).
将A、B、D点的坐标代入解析式,得
$\left\{\begin{array}{l}{4a-2b+c=0}\\{16a+4b+c=0}\\{a+b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-1}\\{c=-4}\end{array}\right.$,
抛物线所对应的二次函数的表达式y=$\frac{1}{2}$x2-x-4;
(2)如图1作C点关于原点的对称点M,
OC=OM=OA=4,
∠OAC=∠MAO=45°,
AP在射线AC与AM之间,∠PAO<45°,
直线AM的解析式为y=-x+4,
联立AM于抛物线,得$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{1}{2}{x}^{2}-x-4}\end{array}\right.$,
解得x=-4或x=4,
∵E点的横坐标是-4,C点的横坐标是0,
P点的横坐标的取值范围是-4≤m≤0;
(3)存在P点,使∠QPO=∠BCO,如图2, ,
,
设P(m,$\frac{1}{2}$m2-m-4),当点P在第二象限时,
由∠QPO=∠BCO,∠PQO=CBO=90°.
∴△PQO∽△COB,
∴$\frac{PQ}{CO}$=$\frac{OQ}{OB}$即$\frac{-m}{4}$=$\frac{\frac{1}{2}{m}^{2}-m-4}{2}$,
化简,得m2-m-8=0.
解得m=$\frac{1-\sqrt{33}}{2}$,m=$\frac{1+\sqrt{33}}{2}$(不符合题意,舍),
$\frac{1}{2}$m2-m-4=$\frac{1}{2}$($\frac{1-\sqrt{33}}{2}$)2-$\frac{1-\sqrt{33}}{2}$-4=$\frac{\sqrt{33}-1}{4}$,
P点坐标为($\frac{1-\sqrt{33}}{2}$,$\frac{\sqrt{33}-1}{4}$).
当点P在第三象限时,同理可得点P为(m,$\frac{1}{2}$m)
代入y=$\frac{1}{2}$x2-x-4,得$\frac{1}{2}$m=$\frac{1}{2}$m2-m-4,解得m=$\frac{3±\sqrt{41}}{2}$,
∵m<0
∴P($\frac{3-\sqrt{41}}{2}$,$\frac{3-\sqrt{41}}{4}$),
∴满足条件的点为P($\frac{1-\sqrt{33}}{2}$,$\frac{\sqrt{33}-1}{4}$),或P($\frac{3-\sqrt{41}}{2}$,$\frac{3-\sqrt{41}}{4}$).
点评 本题考察了二次函数综合题,利用待定系数法求函数解析式,利用了角与对边的关系:角越小角的对边越小得出PA在在射线AC与AM之间是解题关键,利用了相似三角形的判定与性质.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案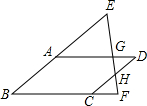 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )| A. | $\frac{EA}{BE}$=$\frac{EG}{EF}$ | B. | $\frac{EG}{GH}$=$\frac{AG}{GD}$ | C. | $\frac{AB}{AE}$=$\frac{BC}{CF}$ | D. | $\frac{FH}{EH}$=$\frac{CF}{AD}$ |
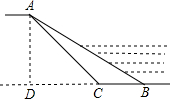 为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少?
为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少? .
.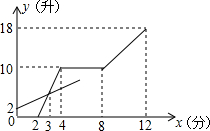 现有甲、乙两个容器,分别装有进水管和出水管,两容器的进出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.
现有甲、乙两个容器,分别装有进水管和出水管,两容器的进出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.