题目内容
2.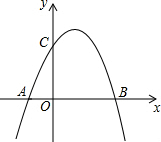 如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0),B(2,0),交y轴于C(0,2),作直线BC.
如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0),B(2,0),交y轴于C(0,2),作直线BC.(1)求二次函数的解析式;
(2)点P在二次函数图象上,且PB=PC,求点P的坐标.
分析 (1)认真审题,将A、B、C三点代入二次函数解析式,据此即可得解;
(2)根据PB=PC,可知点P在线段BC的垂直平分线上,据此即可得解.
解答 解:(1)∵抛物线y=ax2+bx+c经过(2,0),(-1,0),(0,2),由题意得:
$\left\{\begin{array}{l}{0=4a+2b+c}\\{0=a-b+c}\\{2=c}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=-1}\\{b=1}\\{c=2}\end{array}\right.$
∴抛物线的解析式为y=-x2+x+2;
(2)∵PB=PC B(2,0),C(0,2)
∴点P在直线y=x
∴$\left\{\begin{array}{l}{y=x}\\{y=-{x}^{2}+x+2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{x}_{1}=\sqrt{2}}\\{{y}_{1}=\sqrt{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\sqrt{2}}\\{{y}_{2}=-\sqrt{2}}\end{array}\right.$
∴P1($\sqrt{2}$,$\sqrt{2}$),P2(-$\sqrt{2}$,-$\sqrt{2}$).
点评 本题主要考查了运用待定系数法求二次函数的解析式的方法,以及线段的垂直平分线的性质,有一定的综合性,注意总结.

练习册系列答案
相关题目
12.已知关于x的方程(1-2k)x2-2$\sqrt{k+1}$x-1=0有实数根,则k的取值范围是( )
| A. | k≥2 | B. | k≤2 | C. | -1≤k≤2 | D. | -1≤k≤2且$k≠\frac{1}{2}$ |
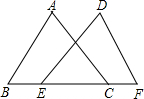 已知,如图,AB=DF,BE=FC,∠B=∠F,求证:△ABC≌△DFE.
已知,如图,AB=DF,BE=FC,∠B=∠F,求证:△ABC≌△DFE. 已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是(22016,0).
已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是(22016,0).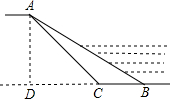 为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少?
为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少? 如图,在平行四边形ABCD中,点E为边AD的中点,连接AC,BE交于点O,则S△AOE:S△COB=1:4.
如图,在平行四边形ABCD中,点E为边AD的中点,连接AC,BE交于点O,则S△AOE:S△COB=1:4.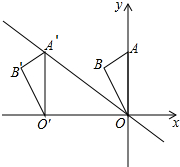 如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线y=-$\frac{3}{4}$x上,则点B与其对应点B′间的距离为8.
如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线y=-$\frac{3}{4}$x上,则点B与其对应点B′间的距离为8. .
.