题目内容
17. 如图,在△ABC中,∠ACB=90°,AB=5,AC=4,过点C作直线MC使得∠BCM=∠BAC,求点B到直线MC的距离.
如图,在△ABC中,∠ACB=90°,AB=5,AC=4,过点C作直线MC使得∠BCM=∠BAC,求点B到直线MC的距离.
分析 利用勾股定理求出BC,过B向MC作垂线,利用三角形相似求BE.
解答 解:如图:在Rt△ABC中,
BC=$\sqrt{{AB}^{2}{-AC}^{2}}$=3,
作BE⊥MC,垂足是E,
∵∠ACB=∠BEC=90°,
∴△ACB∽△BCE,
∴$\frac{AB}{BC}=\frac{BC}{BE}$,
∴$\frac{5}{3}=\frac{3}{BE}$,
∴BE=$\frac{9}{5}$,
∴点B到直线MC的距离$\frac{9}{5}$.
点评 本题考查了相似三角形的判定和性质,勾股定理作辅助线构造相似三角形是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
12.已知关于x的方程(1-2k)x2-2$\sqrt{k+1}$x-1=0有实数根,则k的取值范围是( )
| A. | k≥2 | B. | k≤2 | C. | -1≤k≤2 | D. | -1≤k≤2且$k≠\frac{1}{2}$ |
9.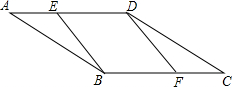 如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
 如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )| A. | AE=CF | B. | BE=DF | C. | ∠EBF=∠FDE | D. | ∠BED=∠BFD |
 如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为36°.
如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为36°.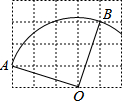 如图,扇形OAB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为$\frac{\sqrt{10}}{4}$.
如图,扇形OAB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为$\frac{\sqrt{10}}{4}$.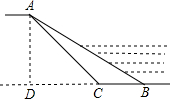 为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少?
为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少?