题目内容
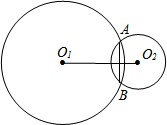 ⊙O1和⊙O2相交于A、B两点,⊙O1的半径为5cm,⊙O2的半径为3
⊙O1和⊙O2相交于A、B两点,⊙O1的半径为5cm,⊙O2的半径为3| 2 |
考点:相交两圆的性质
专题:
分析:根据相交两圆的性质得出AC=
AB,进而利用勾股定理求出OC,再利用勾股定理得出AC的长即可.
| 1 |
| 2 |
解答:解:连接AO1,AO2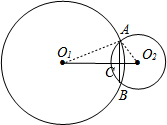
∵⊙O1,⊙O2相交于A、B两点,两圆半径分别为5cm和3
cm,两圆的连心线O1O2的长为7cm,
∴O1O2⊥AB,
∴AC=
AB,
设O1C=x,则O2C=7-x,
∴52-x2=(3
)2-(7-x)2,
解得:x=4,
∴AC2=52-x2=25-42=9,
∴AC=3cm,
∴弦AB的长为:6cm.
故答案为:6cm.

∵⊙O1,⊙O2相交于A、B两点,两圆半径分别为5cm和3
| 2 |
∴O1O2⊥AB,
∴AC=
| 1 |
| 2 |
设O1C=x,则O2C=7-x,
∴52-x2=(3
| 2 |
解得:x=4,
∴AC2=52-x2=25-42=9,
∴AC=3cm,
∴弦AB的长为:6cm.
故答案为:6cm.
点评:此题考查了相交圆的性质与勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
某天,5个同学去打羽毛球,从上午8:55一直到11:55,若这段时间内,一直玩双打(即须4人同时上场),则平均一个人的上场时间为几分钟?( )
| A、36 | B、45 |
| C、135 | D、144 |
 如图,已知点A是一次函数y=x-4图象上的一点,且矩形ABOC的面积等于3,则点A的坐标为
如图,已知点A是一次函数y=x-4图象上的一点,且矩形ABOC的面积等于3,则点A的坐标为 如图,已知在△ABC中,DE∥BC,AE是AF、AC的比例中项,求证:DF∥BE.
如图,已知在△ABC中,DE∥BC,AE是AF、AC的比例中项,求证:DF∥BE.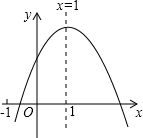 已知二次函数y=ax2+bx+c图象如图所示,下列结论:
已知二次函数y=ax2+bx+c图象如图所示,下列结论: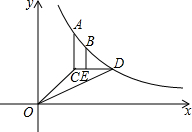 如图,已知反比例函数y=
如图,已知反比例函数y=