题目内容
5．
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，请你根据所学的图形的全等这一章的知识，说明画出∠A′O′B′=∠AOB的依据是（ ）| A． | SAS | B． | SSS | C． | AAS | D． | ASA |
分析 利用画法得到OD=OC=OD′=OC′，CD=C′D′，则根据“SSS”可判定△OCD≌△O′C′D′，然后根据全等三角形的性质可判定∠A′O′B′=∠AOB．
解答 解：由画法得OD=OC=OD′=OC′，CD=C′D′，
所以△OCD≌△O′C′D′（SSS），
所以∠DOC=∠D′O′C′，
即∠A′O′B′=∠AOB．
故选B．
点评 本题考查了基本作图：作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线．
练习册系列答案
相关题目
15．
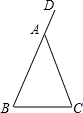如图，在△ABC中，AB=AC，D是BA延长线上的点，现要利用尺规作图过点A作BC的平行线，下列作法不能达到目的是（ ）
如图，在△ABC中，AB=AC，D是BA延长线上的点，现要利用尺规作图过点A作BC的平行线，下列作法不能达到目的是（ ）| A． | 以A点为圆心，以AD长为半径画弧，交AC与点E；再分别以D，E为圆心，再以适当长度为半径画弧，使两弧交于点P；连接AP，则AP为所求直线 | |
| B． | 取AC中点E（作法略），作射线BE，再以E点为圆心，以BE长为半径画弧，交射线BE于另一点P；连接AP，则AP为所求直线 | |
| C． | 作∠B的角平分线（作法略）BM，再以以A点为圆心，以AB长为半径画弧，交射线BM于点P，连接AP，则AP为所求直线 | |
| D． | 将BC向上平移m个单位，让m等于A点到BC的距离，则平移后的线段为所求 |
13．
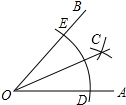如图，下面是利用尺规作∠AOB的角平分线OC的作法：
①以O为圆心，适当长为半径画弧，分别交OA，OB于点D，E；
②分别以D，E为圆心，大于$\frac{1}{2}$DE的长为半径画弧，两弧在∠AOB内交于一点C；
③画射线OC，射线OC就是∠AOB的角平分线．
能说明射线OC是∠AOB的角平分线的依据是（ ）
如图，下面是利用尺规作∠AOB的角平分线OC的作法：①以O为圆心，适当长为半径画弧，分别交OA，OB于点D，E；
②分别以D，E为圆心，大于$\frac{1}{2}$DE的长为半径画弧，两弧在∠AOB内交于一点C；
③画射线OC，射线OC就是∠AOB的角平分线．
能说明射线OC是∠AOB的角平分线的依据是（ ）
| A． | SAS | B． | SSS | C． | ASA | D． | AAS |
△ABC中，∠A=90°，点D在AC边上，DE∥BC，若∠1=55°，则∠B的度数为35°．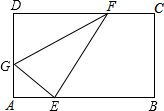
在矩形ABCD中，AB=5，BC=3，如图所示折叠矩形ABCD，使D点落在边AB上一点E处，折痕端点G、F分别在边AD、DC上，则当折痕端点F恰好与C点重合时，AE的长为1cm．
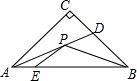如图所示，Rt△ABC中，AC=BC=4，AD平分∠BAC，点E在边AB上，且AE=1，点P是线段AD上的一个动点，则PE+PB的最小值等于5．
15．如图，在数轴上标注了四段范围，则表示$\sqrt{8}$的点落在（ ）
| A． | ①段 | B． | ②段 | C． | ③段 | D． | ④段 |