题目内容
14.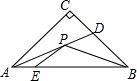 如图所示,Rt△ABC中,AC=BC=4,AD平分∠BAC,点E在边AB上,且AE=1,点P是线段AD上的一个动点,则PE+PB的最小值等于5.
如图所示,Rt△ABC中,AC=BC=4,AD平分∠BAC,点E在边AB上,且AE=1,点P是线段AD上的一个动点,则PE+PB的最小值等于5.
分析 作E关于AD的对称点E′,连接BE′交AD于P,于是得到PE+PB的最小值=BE′,根据勾股定理即可得到结论.
解答  解:作E关于AD的对称点E′,连接BE′交AD于P,
解:作E关于AD的对称点E′,连接BE′交AD于P,
则此时PE+PB有最小值,PE+PB的最小值=BE′,
∴AE′=AE=1,
∵AC=BC=4,
∴CE′=3,
∴BE′=$\sqrt{CE{′}^{2}+B{C}^{2}}$=5,
∴PE+PB的最小值=5,
故答案为:5.
点评 此题主要考查了利用轴对称求最短路径问题以及勾股定理等知识,根据已知得出对应点P位置是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )
 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )| A. | SAS | B. | SSS | C. | AAS | D. | ASA |
2.将△ABC各顶点的横坐标分别加上3,纵坐标不变,得到的△DEF相应顶点的坐标,则△DEF可以看成△ABC( )
| A. | 向左平移3个单位长度得到 | B. | 向右平移三个单位长度得到 | ||
| C. | 向上平移3个单位长度得到 | D. | 向下平移3个单位长度得到 |
9.掷一颗均匀的骰子,掷出的点数是奇数的概率为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{6}$ |
19. 如图,下列条件中,不能推断AB∥CD的是( )
如图,下列条件中,不能推断AB∥CD的是( )
 如图,下列条件中,不能推断AB∥CD的是( )
如图,下列条件中,不能推断AB∥CD的是( )| A. | ∠B=∠5 | B. | ∠1=∠2 | C. | ∠3=∠4 | D. | ∠B+∠BCD=180° |
4.对于“$\sqrt{7}$”,下面说法不正确的是( )
| A. | 它是一个无理数 | |
| B. | 它是数轴上离原点$\sqrt{7}$个单位长度的点表示的数 | |
| C. | 若a<$\sqrt{7}$<a+1,则整数a为2 | |
| D. | 它表示面积为7的正方形的边长 |
 阅读下面材料:在数学课上,老师提出如下问题:尺规作图:
阅读下面材料:在数学课上,老师提出如下问题:尺规作图: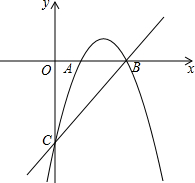 在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线y=kx-3经过B、C两点.
在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线y=kx-3经过B、C两点.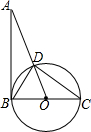 如图,AB=12,且AB为⊙O的切线,BC为⊙O的直径,AO与⊙O交于点D、AD=8.
如图,AB=12,且AB为⊙O的切线,BC为⊙O的直径,AO与⊙O交于点D、AD=8.