题目内容
17．
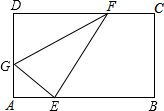在矩形ABCD中，AB=5，BC=3，如图所示折叠矩形ABCD，使D点落在边AB上一点E处，折痕端点G、F分别在边AD、DC上，则当折痕端点F恰好与C点重合时，AE的长为1cm．
分析 首先根据题意画出图形，然后由勾股定理求得BE的长，继而求得答案．
解答 
解：如图，∵在矩形ABCD中，AB=5，BC=3，
∴CD=AB=5，∠B=90°，
由折叠的性质可得：CE=CD=5，
∴BE=$\sqrt{C{E}^{2}-B{C}^{2}}$=4，
∴AE=AB-BE=1．
故答案为：1．
点评 此题考查了折叠的性质、矩形的性质以及勾股定理．注意根据题意画出图形，结合图形求解是关键．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
将一幅三角板如图放置，若AE∥BC，则∠AFD=75度．
5．
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，请你根据所学的图形的全等这一章的知识，说明画出∠A′O′B′=∠AOB的依据是（ ）
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，请你根据所学的图形的全等这一章的知识，说明画出∠A′O′B′=∠AOB的依据是（ ）| A． | SAS | B． | SSS | C． | AAS | D． | ASA |
12．下列命题中，真命题是（ ）
| A． | 两条对角线相等的平行四边形是矩形 | |
| B． | 两条对角线相等的四边形是矩形 | |
| C． | 对角线垂直且相等的四边形是正方形 | |
| D． | 两条对角线垂直的四边形是菱形 |
2．将△ABC各顶点的横坐标分别加上3，纵坐标不变，得到的△DEF相应顶点的坐标，则△DEF可以看成△ABC（ ）
| A． | 向左平移3个单位长度得到 | B． | 向右平移三个单位长度得到 | ||
| C． | 向上平移3个单位长度得到 | D． | 向下平移3个单位长度得到 |
9．掷一颗均匀的骰子，掷出的点数是奇数的概率为（ ）
| A． | 0 | B． | $\frac{1}{2}$ | C． | 1 | D． | $\frac{1}{6}$ |
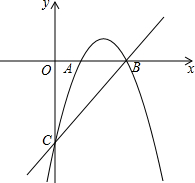在平面直角坐标系xOy中，抛物线y=-x2+bx+c与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点B的坐标为（3，0），直线y=kx-3经过B、C两点．