题目内容
11.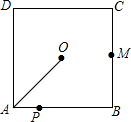 如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A-B-M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )
如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A-B-M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )| A. | 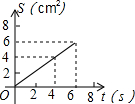 | B. | 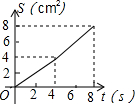 | C. | 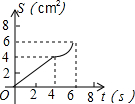 | D. | 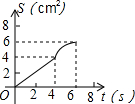 |
分析 分两种情况:①当0≤t<4时,作OG⊥AB于G,由正方形的性质得出∠B=90°,AD=AB=BC=4cm,AG=BG=OG=$\frac{1}{2}$AB=2cm,由三角形的面积得出S=$\frac{1}{2}$AP•OG=t(cm2);
②当t≥4时,S=△OAG的面积+梯形OGBP的面积=t(cm2);得出面积S(cm2)与时间t(s)的关系的图象是过原点的线段,即可得出结论.
解答 解 分两种情况:
分两种情况:
①当0≤t<4时,
作OG⊥AB于G,如图1所示:
∵四边形ABCD是正方形,
∴∠B=90°,AD=AB=BC=4cm,
∵O是正方形ABCD的中心,
∴AG=BG=OG=$\frac{1}{2}$AB=2cm,
∴S=$\frac{1}{2}$AP•OG=$\frac{1}{2}$×t×2=t(cm2),
②当t≥4时,作OG⊥AB于G,
如图2所示:
S=△OAG的面积+梯形OGBP的面积=$\frac{1}{2}$×2×2+$\frac{1}{2}$(2+t-4)×2=t(cm2);
综上所述:面积S(cm2)与时间t(s)的关系的图象是过原点的线段,
故选A.
点评 本题考查了动点问题的函数图象、正方形的性质;熟练掌握正方形的性质,求出S与t的函数关系式是解决问题的关键.

练习册系列答案
相关题目
19.在平面直角坐标系中,把△ABC经过平移得到△A′B′C′,若A(1,m),B(4,2),点A的对应点A′(3,m+2),则点B对应点B′的标为( )
| A. | (6,5) | B. | (6,4) | C. | (5,m) | D. | (6,m) |
16.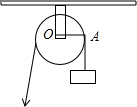 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点A旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点A旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点A旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点A旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )| A. | πcm | B. | 2πcm | C. | 3πcm | D. | 5πcm |
 某通讯运营商的手机上网流量资费标准推出了三种优惠方案:
某通讯运营商的手机上网流量资费标准推出了三种优惠方案: 测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
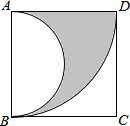 如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则阴影部分面积是2π(结果保留π).
如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则阴影部分面积是2π(结果保留π).