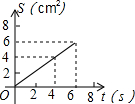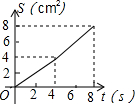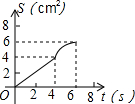题目内容
1. 某通讯运营商的手机上网流量资费标准推出了三种优惠方案:
某通讯运营商的手机上网流量资费标准推出了三种优惠方案:方案A:按流量计费,0.1元/M;
方案B:20元流量套餐包月,包含500M流量,如果超过500M,超过部分按流量计费,如果用到1000M时,超过1000M的流量不再收费;
方案C:120元包月,无限制使用.
用x表示每月上网流量(单位:M),y表示每月的流量费用(单位:元),方案B和方案C对应的y关于x的函数图象如图所示,请解决以下问题:
(1)写出方案A的函数解析式,并在图中画出其图象;
(2)直接写出方案B的函数解析式;
(3)根据三种优惠方案,结合每月的上网流量数,请你给出经济合理的选择方案.
分析 (1)根据流量计费单价即可解决.
(2)根据方案B函数的图象经过(500,20),(1000,130),先求出中间段直线的解析式,再写出分段函数解析式.
(3)画出图象,根据关键点,利用函数图象解决问题.
解答 解:(1)方案A的函数解析式为y=0.1x,图象如图所示.
(2)如图可知方案B函数的图象经过(500,20),(1000,130),
可以求出中间段直线的解析式为y=0.22x-90,
∴方案B的解析式为
y=$\left\{\begin{array}{l}{20}&{(0≤x≤500)}\\{0.22x-90}&{(500<x≤1000)}\\{130}&{(x>1000)}\end{array}\right.$,
(3)如图设方案A的函数图象与方案B的函数图象交于点M、N,与方案C函数图象的交于点Q,则M(200,20),N(750,75),Q(1200,120),
因此,上网流量在200M以下的选用方案A,
上网流量在200M和750M之间的选用方案B,
上网流量在750M和1200M之间的选用方案A,
上网流量在1200以上M的选用方案C,
上网流量在200M或750M的选用方案A或B费用一样,
上网流量是1200M的选用方案A或C费用一样.
点评 本题考查一次函数的应用、分段函数、等知识解题的关键是灵活掌握待定系数法解决问题,学会利用函数图象比较函数值的大小,属于中考常考题型.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
9. 如图所示格点图中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABC缩小,则点C的对应点C′的坐标为( )
如图所示格点图中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABC缩小,则点C的对应点C′的坐标为( )
 如图所示格点图中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABC缩小,则点C的对应点C′的坐标为( )
如图所示格点图中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABC缩小,则点C的对应点C′的坐标为( )| A. | (1,$\frac{3}{2}$) | B. | (2,6) | C. | (2,6)或(-2,-6) | D. | (1,$\frac{3}{2}$)或(-1,-$\frac{3}{2}$) |
6.下列计算结果为正数的是( )
| A. | (-2)-2 | B. | -(-2)0 | C. | -|-2| | D. | (-2)3 |
10.若直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则m的取值范围是( )
| A. | m>2 | B. | m<3 | C. | 2<m<3 | D. | m>3或m<2 |
 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象如图所示,则k的值可能是-1(写一个即可).
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象如图所示,则k的值可能是-1(写一个即可).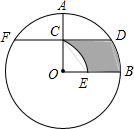 如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=$\sqrt{3}$,以O为圆心,OC为半径作$\widehat{CE}$,交OB于E点.
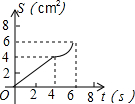
如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=$\sqrt{3}$,以O为圆心,OC为半径作$\widehat{CE}$,交OB于E点.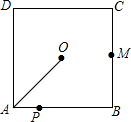 如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A-B-M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )
如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A-B-M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )