题目内容
6. 测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.
分析 (1)由题意可知△BCD是等腰直角三角形,所以BC=DC.
(2)直接利用tan50°=$\frac{AC}{DC}$,进而得出BC的长求出答案.
解答 解:(1)∵∠BDC=45°,∠C=90°,
∴BC=DC=20m,
答:建筑物BC的高度为20m;
(2)设DC=BC=xm,
根据题意可得:tan50°=$\frac{AC}{DC}$=$\frac{5+x}{x}$≈1.2,
解得:x=25,
答:建筑物BC的高度为25m.
点评 此题主要考查了解直角三角形的应用,正确应用锐角三角函数关系是解题关键.

练习册系列答案
相关题目
17. 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{EA}=\frac{DF}{AB}$ | B. | $\frac{DE}{BC}=\frac{EF}{FB}$ | C. | $\frac{BC}{DE}=\frac{BF}{BE}$ | D. | $\frac{BF}{BE}=\frac{BC}{AE}$ |
14.估计$\sqrt{7}$的值介于( )
| A. | 0与1之间 | B. | 1与2之间 | C. | 2与3之间 | D. | 3与4之间 |
1.若m1,m2,…m2016是从0,1,2这三个数中取值的一列数,且m1+m2+…+m2016=1546,(m1-1)2+(m2-1)2+…+(m2016-1)2=1510,则在m1,m2,…m2016中,取值为2的个数为( )
| A. | 505 | B. | 510 | C. | 520 | D. | 550 |
18.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字:昌、爱、我、宜、游、美,现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是( )
| A. | 我爱美 | B. | 宜昌游 | C. | 爱我宜昌 | D. | 美我宜昌 |
15.关于x的一元二次方程:x2-4x-m2=0有两个实数根x1、x2,则m2($\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$)=( )
| A. | $\frac{{m}^{4}}{4}$ | B. | $-\frac{{m}^{4}}{4}$ | C. | 4 | D. | -4 |
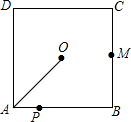 如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A-B-M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )
如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A-B-M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )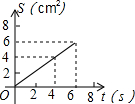
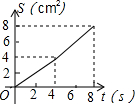
 如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)
如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)