题目内容
2.已知a,b是方程x2+2013x+1=0的两个根,则(1+2015a+a2)(1+2015b+b2)的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据方程的解析式结合根与系数的关系,可得出a+b=-2013,ab=1,根据一元二次方程的解可得出a2+2013a+1=0、b2+2013b+1=0,将其代入(1+2015a+a2)(1+2015b+b2)中即可得出结论.
解答 解:∵a,b是方程x2+2013x+1=0的两个根,
∴a2+2013a+1=0,b2+2013b+1=0,ab=1,a+b=-2013,
∴(1+2015a+a2)(1+2015b+b2)=2a•2b=4ab=4.
故选D.
点评 本题考查了一元二次方程的解以及根与系数的关系,根据一元二次方程的解以及根与系数的关系找出a2+2013a+1=0、b2+2013b+1=0、ab=1是解题的关键.

练习册系列答案
相关题目
10.若直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则m的取值范围是( )
| A. | m>2 | B. | m<3 | C. | 2<m<3 | D. | m>3或m<2 |
17. 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{EA}=\frac{DF}{AB}$ | B. | $\frac{DE}{BC}=\frac{EF}{FB}$ | C. | $\frac{BC}{DE}=\frac{BF}{BE}$ | D. | $\frac{BF}{BE}=\frac{BC}{AE}$ |
7.二元一次方程组$\left\{\begin{array}{l}{x-2y=5}\\{5x+4y=-3}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-\frac{7}{5}}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=-\frac{3}{2}}\end{array}\right.$ |
14.估计$\sqrt{7}$的值介于( )
| A. | 0与1之间 | B. | 1与2之间 | C. | 2与3之间 | D. | 3与4之间 |
 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象如图所示,则k的值可能是-1(写一个即可).
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象如图所示,则k的值可能是-1(写一个即可).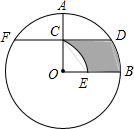 如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=$\sqrt{3}$,以O为圆心,OC为半径作$\widehat{CE}$,交OB于E点.
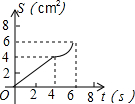
如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=$\sqrt{3}$,以O为圆心,OC为半径作$\widehat{CE}$,交OB于E点.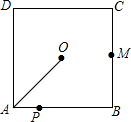 如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A-B-M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )
如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A-B-M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )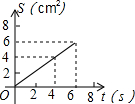
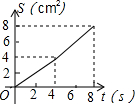
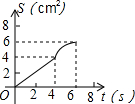
 如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将$\widehat{CD}$沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将$\widehat{CD}$沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC