题目内容
3.阅读理解:我们知道,四边形具有不稳定性,容易变形,如图1,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把$\frac{1}{sinα}$的值叫做这个平行四边形的变形度.
(1)若矩形发生变形后的平行四边形有一个内角是120度,则这个平行四边形的变形度是$\frac{2\sqrt{3}}{3}$.
猜想证明:
(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2,$\frac{1}{sinα}$之间的数量关系,并说明理由;
拓展探究:
(3)如图2,在矩形ABCD中,E是AD边上的一点,且AB2=AE•AD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4$\sqrt{m}$(m>0),平行四边形A1B1C1D1的面积为2$\sqrt{m}$(m>0),试求∠A1E1B1+∠A1D1B1的度数.

分析 (1)根据平行四边形的性质得到α=60°,根据三角函数的定义即可得到结论;
(2)如图1,设矩形的长和宽分别为a,b,变形后的平行四边形的高为h,根据平行四边形和矩形的面积公式即可得到结论;
(3)由已知条件得到△B1A1E1∽△D1A1B1,由相似三角形的性质得到∠A1B1E1=∠A1D1B1,根据平行线的性质得到∠A1E1B1=∠C1B1E1,求得∠A1E1B1+∠A1D1B1=∠C1E1B1+∠A1B1E1=∠A1B1C1,证得∠A1B1C1=30°,于是得到结论.
解答  解:(1)∵平行四边形有一个内角是120度,
解:(1)∵平行四边形有一个内角是120度,
∴α=60°,
∴$\frac{1}{sinα}$=$\frac{1}{sin60°}$=$\frac{2\sqrt{3}}{3}$;
故答案为:$\frac{2\sqrt{3}}{3}$;
(2)$\frac{1}{sinα}$=$\frac{{S}_{1}}{{S}_{2}}$,
理由:如图1,设矩形的长和宽分别为a,b,变形后的平行四边形的高为h,∴S1=ab,S2=ah,sinα=$\frac{h}{b}$,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{ab}{ah}$=$\frac{b}{h}$,∵$\frac{1}{sinα}$=$\frac{b}{h}$,∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{sinα}$;
(3)∵AB2=AE•AD,
∴A1B12=A1E1•A1D1,即$\frac{{A}_{1}{B}_{1}}{{A}_{1}{D}_{1}}$=$\frac{{A}_{1}{E}_{1}}{{A}_{1}{B}_{1}}$,
∵∠B1A1E1=∠D1A1B1,
∴△B1A1E1∽△D1A1B1,
∴∠A1B1E1=∠A1D1B1,
∵A1D1∥B1C1,
∴∠A1E1B1=∠C1B1E1,
∴∠A1E1B1+∠A1D1B1=∠C1B1E1+∠A1B1E1=∠A1B1C1,
由(2)知$\frac{1}{sinα}$=$\frac{{S}_{1}}{{S}_{2}}$可知$\frac{1}{sin∠{A}_{1}{B}_{1}{C}_{1}}$=$\frac{4\sqrt{m}}{2\sqrt{m}}$=2,
∴sin∠A1B1C1=$\frac{1}{2}$,
∴∠A1B1C1=30°,
∴∠A1E1B1+∠A1D1B1=30°.
点评 本题考查了平行四边形的性质,矩形的性质,三角函数的定义,相似三角形的判定和性质,正确的理解题意是解题的关键.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案| A. | 0与1之间 | B. | 1与2之间 | C. | 2与3之间 | D. | 3与4之间 |
| A. | 我爱美 | B. | 宜昌游 | C. | 爱我宜昌 | D. | 美我宜昌 |
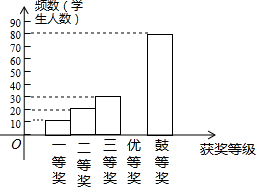 国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:| 获奖等次 | 频数 | 频率 |
| 一等奖 | 10 | 0.05 |
| 二等奖 | 20 | 0.10 |
| 三等奖 | 30 | b |
| 优胜奖 | a | 0.30 |
| 鼓励奖 | 80 | 0.40 |
(1)a=60,b=0.15,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
| A. | $\frac{{m}^{4}}{4}$ | B. | $-\frac{{m}^{4}}{4}$ | C. | 4 | D. | -4 |
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 有两边及一角对应相等的两个三角形全等 | |
| C. | 矩形的对角线相等 | |
| D. | 平行四边形是轴对称图形 |
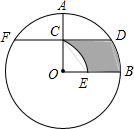 如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=$\sqrt{3}$,以O为圆心,OC为半径作$\widehat{CE}$,交OB于E点.
如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=$\sqrt{3}$,以O为圆心,OC为半径作$\widehat{CE}$,交OB于E点.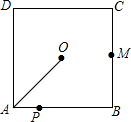 如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A-B-M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )
如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A-B-M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )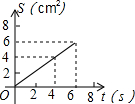
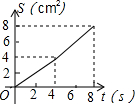
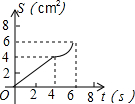
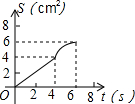
 如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将$\widehat{CD}$沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将$\widehat{CD}$沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC