题目内容
1．
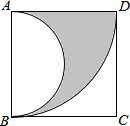如图，在边长为4的正方形ABCD中，先以点A为圆心，AD的长为半径画弧，再以AB边的中点为圆心，AB长的一半为半径画弧，则阴影部分面积是2π（结果保留π）．
分析 根据题意有S阴影部分=S扇形BAD-S半圆BA，然后根据扇形的面积公式：S=$\frac{nπ{R}^{2}}{360}$和圆的面积公式分别计算扇形和半圆的面积即可．
解答 解：根据题意得，S阴影部分=S扇形BAD-S半圆BA，
∵S扇形BAD=$\frac{90π•{4}^{2}}{360}$=4π，
S半圆BA=$\frac{1}{2}$•π•22=2π，
∴S阴影部分=4π-2π=2π．
故答案为2π．
点评 此题考查了扇形的面积公式：S=$\frac{nπ{R}^{2}}{360}$，其中n为扇形的圆心角的度数，R为圆的半径），或S=$\frac{1}{2}$lR，l为扇形的弧长，R为半径．
练习册系列答案
相关题目
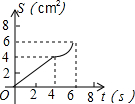
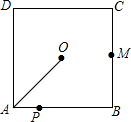如图，O是边长为4cm的正方形ABCD的中心，M是BC的中点，动点P由A开始沿折线A-B-M方向匀速运动，到M时停止运动，速度为1cm/s．设P点的运动时间为t（s），点P的运动路径与OA、OP所围成的图形面积为S（cm2），则描述面积S（cm2）与时间t（s）的关系的图象可以是（ ）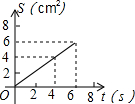
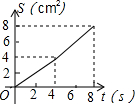
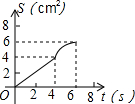
如图，已知⊙O的半径为2，AB为直径，CD为弦．AB与CD交于点M，将$\widehat{CD}$沿CD翻折后，点A与圆心O重合，延长OA至P，使AP=OA，连接PC
如图，在矩形ABCD中，AB=5，BC=10$\sqrt{3}$，一圆弧过点B和点C，且与AD相切，则图中阴影部分面积为75$\sqrt{3}$-$\frac{100π}{3}$．
如图，是某市一座人行天桥的示意图，天桥离地面的高BC是10米，坡面10米处有一建筑物HQ，为了方便使行人推车过天桥，市政府部门决定降低坡度，使新坡面DC的倾斜角∠BDC=30°，若新坡面下D处与建筑物之间需留下至少3米宽的人行道，问该建筑物是否需要拆除（计算最后结果保留一位小数）．（参考数据：$\sqrt{2}$=1.414，$\sqrt{3}$=1.732）
6．如果关于x的一元二次方程x2-6x+2k=0有两个实数根，那么实数k的取值范围是（ ）
| A． | $k≤\frac{9}{2}$ | B． | $k＜\frac{9}{2}$ | C． | $k≥\frac{9}{2}$ | D． | $k＞\frac{9}{2}$ |
13．下列语句正确的是（ ）
| A． | 对角线互相垂直的四边形是菱形 | |
| B． | 有两边及一角对应相等的两个三角形全等 | |
| C． | 矩形的对角线相等 | |
| D． | 平行四边形是轴对称图形 |
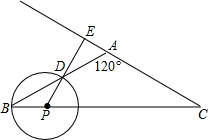如图，△ABC中，∠BAC=120°，AB=AC=6．P是底边BC上的一个动点（P与B、C不重合），以P为圆心，PB为半径的⊙P与射线BA交于点D，射线PD交射线CA于点E．