Question

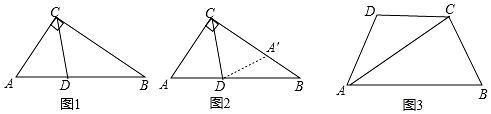
3．如图1，在Rt△ABC中，∠ACB=90°，∠A=60°，CD平分∠ACB，试判断BC和AC、AD之间的数量关系．
小明发现，利用轴对称做一个变化，在BC上截取CA′=CA，连接DA′，得到一对全等的三角形，从而将问题解决（如图2）．请回答：
（1）BC和AC、AD之间的数量关系并证明．
（2）参考上述思考问题的方法，解决下列问题：如图3，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9．求AB的长．

Answer 1

分析 （1）根据SAS证明△ADC≌△A′DC，根据△ADC≌△A′DC，得出DA′=DA，∠CA′D=∠A=60°，得∠CDA′=∠CDA=75°，得∠BDA′=30°=∠B，则DA′=BA′，BA′=AD，从而得出BC=AC+AD．
（2）在AB上截取AE=AD，连接CE，先证明△ADC≌△AEC，得出AE=AD=9，CE=CD=10=BC，过点C作CF⊥AB于点F，设EF=BF=x；在Rt△CFB和Rt△CFA中，根据勾股定理求出x，即可得出结果．

解答 解：（1）BC=AC+AD；   
证明：如图2，∵CD平分∠ACB，
∴∠ACD=∠A′CD，
在△ADC和△A′DC中，
$\left\{\begin{array}{l}{CA′=CA}\\{∠ACD=∠A′CD}\\{CD=CD}\end{array}\right.$，
∴△ADC≌△A′DC（SAS）；        
∴DA′=DA，∠CA′D=∠A=60°，
∵∠ACB=90°，
∴∠B=90°-∠A=30°，
∵∠CA′D=∠B+∠BDA′，
∴∠BDA′=30°=∠B，
∴DA′=BA′，
∴BA′=AD，
∴BC=CA′+BA′=AC+AD；       

（2）如图3，在AB上截取AE=AD，连接CE，
∵AC平分∠BAD，
∴∠DAC=∠EAC．
在△AEC和△ADC中，
$\left\{\begin{array}{l}{CA′=CA}\\{∠DAC=∠EAC}\\{AC=AC}\end{array}\right.$，
∴△ADC≌△AEC（SAS），
∴AE=AD=9，CE=CD=10=BC，
如图，过点C作CF⊥AB于点F，
∴EF=BF，
设EF=BF=x．
在Rt△CFB中，∠CFB=90°，由勾股定理得CF²=CB²-BF²=10²-x²，
在Rt△CFA中，∠CFA=90°，由勾股定理得CF²=AC²-AF²=17²-（9+x）²．
∴10²-x²=17²-（9+x）²，
解得：x=6，
∴AB=AE+EF+FB=9+6+6=21，
∴AB的长为21．

点评 本题属于三角形综合题，主要考查了全等三角形的判定与性质、勾股定理、等腰三角形的判定与性质的综合应用，解题时需要通过作辅助线构造全等三角形，根据全等三角形的对应边相等才能得出结果．