题目内容
18.在-0.101001,$\sqrt{7}$,$\frac{1}{4}$,-$\frac{π}{2}$,0.2121121112…中,无理数的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 无理数就是无限不循环小数,根据定义即可判断.
解答 解:无理数有$\sqrt{7}$,-$\frac{π}{2}$,0.2121121112…,共3个.
故选C.
点评 此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,$\sqrt{6}$,0.8080080008…(每两个8之间依次多1个0)等形式.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
8. 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=25°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=25°,则∠E的度数为( )
 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=25°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=25°,则∠E的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
9.在解方程 $\frac{x-1}{2}$-$\frac{2x+3}{3}$=1 时,去分母正确的是( )
| A. | 3(x-1)-4x+3=1 | B. | 3x-1-4x+3=6 | C. | 3x-1-4x+3=1 | D. | 3(x-1)-2(2x+3)=6 |
13.关于x的一元二次方程kx2-6x+1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k<9且k≠0 | B. | k<9 | C. | k≤9且k≠0 | D. | k≥9 |
7.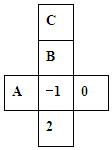 如图是一个正方体纸盒的表面展开图,若在其中三个正方形A、B、C内分别填入适当的数,使它折成正方体后相对的面上的两数互为相反数,则填在正方形A、B、C内的三个数依次为( )
如图是一个正方体纸盒的表面展开图,若在其中三个正方形A、B、C内分别填入适当的数,使它折成正方体后相对的面上的两数互为相反数,则填在正方形A、B、C内的三个数依次为( )
 如图是一个正方体纸盒的表面展开图,若在其中三个正方形A、B、C内分别填入适当的数,使它折成正方体后相对的面上的两数互为相反数,则填在正方形A、B、C内的三个数依次为( )
如图是一个正方体纸盒的表面展开图,若在其中三个正方形A、B、C内分别填入适当的数,使它折成正方体后相对的面上的两数互为相反数,则填在正方形A、B、C内的三个数依次为( )| A. | -2,1,0 | B. | 1,-2,0 | C. | 0,-2,1 | D. | -2,0,1 |
 如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,按此做法进行下去,∠EA3A2的度数为20°,∠A的度数为80°.
如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,按此做法进行下去,∠EA3A2的度数为20°,∠A的度数为80°.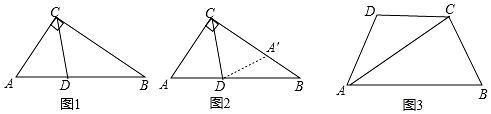
 如图,已知AB=CD,AB∥CD,BE=CF,求证:AF∥ED.
如图,已知AB=CD,AB∥CD,BE=CF,求证:AF∥ED.