题目内容
6. 如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,按此做法进行下去,∠EA3A2的度数为20°,∠A的度数为80°.
如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,按此做法进行下去,∠EA3A2的度数为20°,∠A的度数为80°.
分析 先根据等腰三角形的性质求出∠A与∠BA1A的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠CA2A1,∠DA3A2.
解答 解:∵在△ABA1中,∠B=20°,AB=A1B,
∴∠A=∠BA1A=$\frac{180°-∠B}{2}$=$\frac{180°-20°}{2}$=80°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠CA2A1=$\frac{∠B{A}_{1}A}{2}$=$\frac{80°}{2}$=40°;
同理可得,∠EA3A2=20°,
故答案为:20° 80°.
点评 本题考查的是等腰三角形的性质及三角形外角的性质,找出规律是解答此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
17.下列说法正确的是( )
| A. | 90°的角叫余角,180°的角叫补角 | |
| B. | 如果∠α>∠β,那么∠α的补角比∠β的补角大 | |
| C. | 最小的正整数是1 | |
| D. | 一个数的相反数一定比它本身小 |
14.⊙O的半径为6cm,点A到圆心O的距离为5cm,那么点A与⊙O的位置关系是( )
| A. | 点A在圆内 | B. | 点A在圆上 | C. | 点A在圆外 | D. | 不能确定 |
16. 正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则S9的值为( )
正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则S9的值为( )
 正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则S9的值为( )
正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则S9的值为( )| A. | ${({\frac{1}{2}})^9}$ | B. | ${({\frac{1}{2}})^8}$ | C. | ${({\frac{{\sqrt{2}}}{2}})^9}$ | D. | ${({\frac{{\sqrt{2}}}{2}})^8}$ |
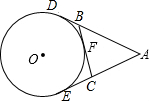 如图,AE,AD,BC分别切⊙O于点E、D和点F,若AD=8cm,则△ABC的周长为16cm.
如图,AE,AD,BC分别切⊙O于点E、D和点F,若AD=8cm,则△ABC的周长为16cm.
 在平面直角坐标系中,$A(6\sqrt{3},0),B(0,6)$,动点M从点O开始沿OA以$\sqrt{3}$cm/s的速度向点A移动,动点N从点A开始沿AB以2cm/s的速度向点B移动.如果M,N分别从O,A同时移动,移动时间为t(0<t<6).
在平面直角坐标系中,$A(6\sqrt{3},0),B(0,6)$,动点M从点O开始沿OA以$\sqrt{3}$cm/s的速度向点A移动,动点N从点A开始沿AB以2cm/s的速度向点B移动.如果M,N分别从O,A同时移动,移动时间为t(0<t<6).