题目内容
1．
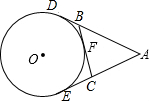如图，AE，AD，BC分别切⊙O于点E、D和点F，若AD=8cm，则△ABC的周长为16cm．
分析 由切线长定理可得AD=AC，DB=BF，CE=CF，则可求得△ABC的周长．
解答 解：
∵AE，AD，BC分别切⊙O于点E、D和点F，
∴AD=AC，DB=BF，CE=CF，
∴AB+BC+AC=AB+BF+CF+AC=AB+BD+CE+AC=AD+AE=2AD=16cm，
故答案为：16．
点评 本题主要考查切线的性质，掌握切线长定理是解题的关键，即从圆外一点引圆的两条切线，它们的切线长相等．
练习册系列答案
状元坊全程突破导练测系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
9．在解方程 $\frac{x-1}{2}$-$\frac{2x+3}{3}$=1 时，去分母正确的是（ ）
| A． | 3（x-1）-4x+3=1 | B． | 3x-1-4x+3=6 | C． | 3x-1-4x+3=1 | D． | 3（x-1）-2（2x+3）=6 |
16．二次函数y=x2的图象向右平移2个单位，得到新的函数图象的表达式是（ ）
| A． | y=x2-2 | B． | y=（x-2）2 | C． | y=x2+2 | D． | y=（x+2）2 |
如图，在△ABA1中，∠B=20°，AB=A1B，在A1B上取一点C，延长AA1到A2，使得A1A2=A1C，在A2C上取一点D，延长A1A2到A3，使得A2A3=A2D，按此做法进行下去，∠EA3A2的度数为20°，∠A的度数为80°．
13．关于x的一元二次方程kx2-6x+1=0有两个不相等的实数根，则k的取值范围是（ ）
| A． | k＜9且k≠0 | B． | k＜9 | C． | k≤9且k≠0 | D． | k≥9 |
如图，已知AB=CD，AB∥CD，BE=CF，求证：AF∥ED．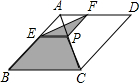
如图所示，菱形ABCD的对角线的长分别为4和6，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是6．