Question

16．已知在矩形ABCD中，AB=2，AE平分∠BAD交BC于点E（点E不与点C重合），连接ED，若△AED是等腰三角形，则AD的长为4．

Answer 1

分析 当AE=DE，在矩形ABCD中，由AE平分∠BAD，得到△ABE是等腰直角三角形，求得AB=BE=2，得到AE=2$\sqrt{2}$，根据全等三角形的性质得到∠DEC=∠AEB=45°，得到∠AED=90°，于是得到结论；如图2，当AD=DE，在矩形ABCD中，于是得到AD=AE=2$\sqrt{2}$．

解答 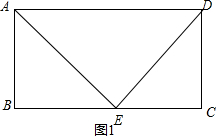解：如图1，当AE=DE，
在矩形ABCD中，
∵AE平分∠BAD，
∴∠BAE=45°，
∴△ABE是等腰直角三角形，
∴AB=BE=2，
∴AE=2$\sqrt{2}$，
在Rt△ABE与Rt△CDE中，$\left\{\begin{array}{l}{AE=DE}\\{AB=CD}\end{array}\right.$，
∴Rt△ABE≌Rt△CDE，
∴∠DEC=∠AEB=45°，
∴∠AED=90°，
∵DE=AE，
∴AD=$\sqrt{2}$AE=4；
如图2，当AD=DE，
在矩形ABCD中，
∵AE平分∠BAD，
∴∠BAE=45°，
∴△ABE是等腰直角三角形，
∴AB=BE=2，
∴AD=AE=2$\sqrt{2}$，
故答案为：4或2$\sqrt{2}$．

点评 本题考查了矩形的性质，全等三角形的判定和性质，等腰直角三角形的性质，正确的作出图形是解题的关键．