题目内容
16. 正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则S9的值为( )
正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则S9的值为( )| A. | ${({\frac{1}{2}})^9}$ | B. | ${({\frac{1}{2}})^8}$ | C. | ${({\frac{{\sqrt{2}}}{2}})^9}$ | D. | ${({\frac{{\sqrt{2}}}{2}})^8}$ |
分析 根据等腰直角三角形的性质可得出S2+S2=S1,写出部分Sn的值,根据数的变化找出变化规律Sn=($\frac{1}{2}$)n-1,依此规律即可得出结论.
解答 解:在图中标上字母E,如图所示.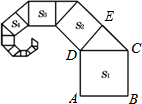
∵正方形ABCD的边长为1,△CDE为等腰直角三角形,
∴DE2+CE2=CD2,DE=CE,
∴S2+S2=S1.
观察,发现规律:S1=12=1,S2=$\frac{1}{2}$S1=$\frac{1}{2}$,S3=$\frac{1}{2}$S2=$\frac{1}{4}$,S4=$\frac{1}{2}$S3=$\frac{1}{8}$,…,
∴Sn=($\frac{1}{2}$)n-1.
当n=9时,S9=($\frac{1}{2}$)9-1=($\frac{1}{2}$)8,
故选:B.
点评 本题考查了等腰直角三角形的性质、勾股定理以及规律型中数的变化规律,解题的关键是找出规律Sn=($\frac{1}{2}$)n-1.本题属于中档题,难度不大,解决该题型题目时,写出部分Sn的值,根据数值的变化找出变化规律是关键.

练习册系列答案
相关题目
7.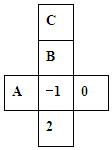 如图是一个正方体纸盒的表面展开图,若在其中三个正方形A、B、C内分别填入适当的数,使它折成正方体后相对的面上的两数互为相反数,则填在正方形A、B、C内的三个数依次为( )
如图是一个正方体纸盒的表面展开图,若在其中三个正方形A、B、C内分别填入适当的数,使它折成正方体后相对的面上的两数互为相反数,则填在正方形A、B、C内的三个数依次为( )
 如图是一个正方体纸盒的表面展开图,若在其中三个正方形A、B、C内分别填入适当的数,使它折成正方体后相对的面上的两数互为相反数,则填在正方形A、B、C内的三个数依次为( )
如图是一个正方体纸盒的表面展开图,若在其中三个正方形A、B、C内分别填入适当的数,使它折成正方体后相对的面上的两数互为相反数,则填在正方形A、B、C内的三个数依次为( )| A. | -2,1,0 | B. | 1,-2,0 | C. | 0,-2,1 | D. | -2,0,1 |
 如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,按此做法进行下去,∠EA3A2的度数为20°,∠A的度数为80°.
如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,按此做法进行下去,∠EA3A2的度数为20°,∠A的度数为80°.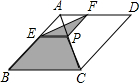 如图所示,菱形ABCD的对角线的长分别为4和6,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是6.
如图所示,菱形ABCD的对角线的长分别为4和6,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是6.
 在行驶完某段全程600千米的高速公路时,李师傅对张师傅说:“你的车速太快了,平均每小时比我多跑20千米,比我少用1.5小时就跑完了全程.”
在行驶完某段全程600千米的高速公路时,李师傅对张师傅说:“你的车速太快了,平均每小时比我多跑20千米,比我少用1.5小时就跑完了全程.”