题目内容
9. 如图,在△ABC中,∠ABC=65°,∠ACB=45°,BE,CF分别是边AC,AB上的高,BE,CF分别相交于点H,求∠BHC的度.
如图,在△ABC中,∠ABC=65°,∠ACB=45°,BE,CF分别是边AC,AB上的高,BE,CF分别相交于点H,求∠BHC的度.
分析 先根据三角形内角和定理计算出∠A=180°-∠ABC-∠ACB=62°,再根据高的定义得∠AEB=∠AFC=90°,于是利用四边形内角和为360°可计算出∠EHF=118°,然后根据对顶角相等得到∠BHC的度数.
解答 解:∵∠ABC=65°,∠ACB=45°,
∴∠A=180°-∠ABC-∠ACB=70°,
∵BE、CF是两边AC、AB上的高,
∴∠AEB=∠AFC=90°,
而∠A+∠AFH+∠AEH+∠EHF=360°,
∴∠EHF=180°-70°=110°,
∴∠BHC=110°.
点评 本题考查了三角形内角和定理:三角形内角和是180°,高的定义,以及四边形内角和为360°,注意角的运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10…%的比例计算甲、乙的平均成绩,那么谁将胜出?
| 选手 | 演讲内容 | 演讲能力 | 演讲效果 |
| 甲 | 85 | 95 | 95 |
| 乙 | 95 | 85 | 95 |
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10…%的比例计算甲、乙的平均成绩,那么谁将胜出?
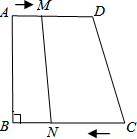 如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则:
如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则:
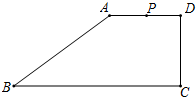 已知在梯形ABCD中,AD∥BC,∠ADC=90°,且AD=DC=3cm,AB=5cm,动点P从A点出发,以1cm/s的速度沿折线A-D-C运动,过点P作PQ∥AB,交BC于点Q,设运动时间为t(s),
已知在梯形ABCD中,AD∥BC,∠ADC=90°,且AD=DC=3cm,AB=5cm,动点P从A点出发,以1cm/s的速度沿折线A-D-C运动,过点P作PQ∥AB,交BC于点Q,设运动时间为t(s),