题目内容
20.先化简,再求值:[(a-b)2+(2a+b)(1-b)]÷(-$\frac{1}{2}$a),其中a,b满足|a+1|+|2b-1|2=0.分析 首先根据非负数的性质求出a和b的值,然后根据多项式乘法的运算法则去掉括号,再进行化简,最后代值计算.
解答 解:∵|a+1|+|2b-1|2=0,
∴a+1=0且2b-1=0,
∴a=-1,b=$\frac{1}{2}$,
原式=(a2-2ab+b2+2a-2ab+b-b2)×(-$\frac{2}{a}$)
=(a2-4ab+2a+b)(-$\frac{2}{a}$)
=-2a+8b-4-$\frac{2b}{a}$,
所以把a=-1,b=$\frac{1}{2}$代入化简的式子中得到原式=2+4-4+1=3.
点评 本题主要考查了整式的混合运算-化简求值的知识,解答本题的关键是根据非负数的性质求出a和b的值,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.菱形的周长为4,一个内角为60°,则较短的对角线长为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
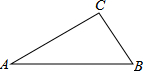 在△ABC中,∠ACB=90°,若∠A=30°,CA=6,则AB的长为,4$\sqrt{3}$,△ABC的面积为6$\sqrt{3}$.
在△ABC中,∠ACB=90°,若∠A=30°,CA=6,则AB的长为,4$\sqrt{3}$,△ABC的面积为6$\sqrt{3}$.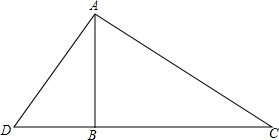 如图所示,一棵32米高的巨大杉树在海棠号台风中被刮断,树顶C落在离树根B点16米处,科研人员要看查看断痕A处的情况,在离树根B有5米的D处竖起一个梯子AD,请问这个梯子有多长?
如图所示,一棵32米高的巨大杉树在海棠号台风中被刮断,树顶C落在离树根B点16米处,科研人员要看查看断痕A处的情况,在离树根B有5米的D处竖起一个梯子AD,请问这个梯子有多长? 如图,在△ABC中,∠ABC=65°,∠ACB=45°,BE,CF分别是边AC,AB上的高,BE,CF分别相交于点H,求∠BHC的度.
如图,在△ABC中,∠ABC=65°,∠ACB=45°,BE,CF分别是边AC,AB上的高,BE,CF分别相交于点H,求∠BHC的度.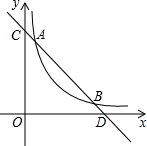 如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A、B两点,与x轴、y轴分别交于C、D两点.
如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A、B两点,与x轴、y轴分别交于C、D两点.