题目内容
19.已知$\frac{\sqrt{3}+1}{\sqrt{3}-1}$的整数部分为m,小数部分为n,求m2-$\sqrt{3}mn+{n}^{2}$的值.分析 根据1<$\sqrt{3}$<2,可得m,n的值,根据代数式求值,可得答案.
解答 解:由1<$\sqrt{3}$<2,得m=3,n=$\frac{\sqrt{3}+1}{\sqrt{3}-1}$-3,
m2-$\sqrt{3}mn+{n}^{2}$=32-3$\sqrt{3}$($\frac{4-2\sqrt{3}}{\sqrt{3}-1}$)+($\frac{4-2\sqrt{3}}{\sqrt{3}-1}$)2
=9-$\frac{12\sqrt{3}-18}{\sqrt{3}-1}$+4-2$\sqrt{3}$
=9-(9-3$\sqrt{3}$)+4-2$\sqrt{3}$
=$\sqrt{3}$+4.
点评 本题考查了估算无理数的大小,利用1<$\sqrt{3}$<2,得出m,n的值是解题关键,注意要分母有理化.

练习册系列答案
相关题目
9.下列运算正确的是( )
| A. | x6•x2=x12 | B. | x6÷x2=x3 | C. | (x2)3=x5 | D. | x2+x2=2x2 |
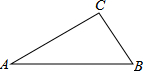 在△ABC中,∠ACB=90°,若∠A=30°,CA=6,则AB的长为,4$\sqrt{3}$,△ABC的面积为6$\sqrt{3}$.
在△ABC中,∠ACB=90°,若∠A=30°,CA=6,则AB的长为,4$\sqrt{3}$,△ABC的面积为6$\sqrt{3}$.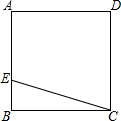 如图,ABCD是一块正方形的场地,小华和小芳在AB边上选定了一点E,测量知EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
如图,ABCD是一块正方形的场地,小华和小芳在AB边上选定了一点E,测量知EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?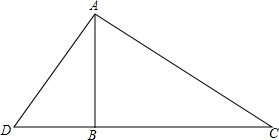 如图所示,一棵32米高的巨大杉树在海棠号台风中被刮断,树顶C落在离树根B点16米处,科研人员要看查看断痕A处的情况,在离树根B有5米的D处竖起一个梯子AD,请问这个梯子有多长?
如图所示,一棵32米高的巨大杉树在海棠号台风中被刮断,树顶C落在离树根B点16米处,科研人员要看查看断痕A处的情况,在离树根B有5米的D处竖起一个梯子AD,请问这个梯子有多长? 如图,在△ABC中,∠ABC=65°,∠ACB=45°,BE,CF分别是边AC,AB上的高,BE,CF分别相交于点H,求∠BHC的度.
如图,在△ABC中,∠ABC=65°,∠ACB=45°,BE,CF分别是边AC,AB上的高,BE,CF分别相交于点H,求∠BHC的度.