题目内容
14.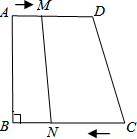 如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则:
如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则:(1)几秒后四边形MNCD为平行四边形;
(2)几秒后四边形ABNM为矩形.
分析 (1)用t表示出MD、CN,然后根据平行四边形对边相等可得MD=CN,然后计算即可得解;
(2)表示出AM和BN的长,当AM=BN时四边形ABNM为矩形.
解答 解:(1)设t秒后四边形MNCD为平行四边形,
∵点M的速度为1cm/s,点N的速度为2cm/s,
∴MD=AD-AM=18-t,CN=2t,
四边形MNCD是平行四边形时,MD=CN,
∴18-t=2t,
解得t=6;
∴6秒时,四边形MNCD是平行四边形;
(2)根据题意得:AM=t,BN=21-2t,
当四边形ABNM为矩形时AM=BN,
即:t=21-2t,
解得:t=7,
∴7秒时,四边形ABNM为矩形.
点评 本题考查了梯形,平行四边形的性质,直角梯形的性质,等腰梯形的性质及矩形的判定,熟练掌握各图形的性质,分别列出关于t的方程是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.菱形的周长为4,一个内角为60°,则较短的对角线长为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
9.一个病人每天下午需要测量血压,该病人上周日的收缩压为120单位,下表是该病人这周一到周五与前一天相比较收缩压的变化情况:
本周星期二的收缩压是( )
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 增减 | +20 | -30 | -25 | +15 | +30 |
| A. | 110 | B. | 120 | C. | 125 | D. | 130 |
 如图,四边形ABCD是正方形,△CDE是等边三角形,则∠AEB=150°.
如图,四边形ABCD是正方形,△CDE是等边三角形,则∠AEB=150°. 如图,在△ABC中,∠ABC=65°,∠ACB=45°,BE,CF分别是边AC,AB上的高,BE,CF分别相交于点H,求∠BHC的度.
如图,在△ABC中,∠ABC=65°,∠ACB=45°,BE,CF分别是边AC,AB上的高,BE,CF分别相交于点H,求∠BHC的度.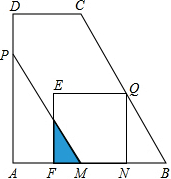 如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=AD=10,CD=5,动点P从点A出发,沿折线AD-DC以每秒4个单位的速度向点C运动;点Q从点B出发,沿线段BC以每秒$\sqrt{5}$个单位的速度向点C运动,P,Q两点同时出发,当其中一点到达终点时,另一点也停止运动,过点P作PM∥BC交AB于M,过点Q作QN⊥AB交AB于N,以线段QN为一边在QN的左侧作正方形QEFN,设运动时间为t(s),线段PM扫过平面部分与正方形QEFN重叠部分的面积为S.
如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=AD=10,CD=5,动点P从点A出发,沿折线AD-DC以每秒4个单位的速度向点C运动;点Q从点B出发,沿线段BC以每秒$\sqrt{5}$个单位的速度向点C运动,P,Q两点同时出发,当其中一点到达终点时,另一点也停止运动,过点P作PM∥BC交AB于M,过点Q作QN⊥AB交AB于N,以线段QN为一边在QN的左侧作正方形QEFN,设运动时间为t(s),线段PM扫过平面部分与正方形QEFN重叠部分的面积为S. 根据机器零件的设计图纸(如图),用不等式表示零件长度的合格尺寸(L的取值范围)19.99≤L≤20.01.
根据机器零件的设计图纸(如图),用不等式表示零件长度的合格尺寸(L的取值范围)19.99≤L≤20.01.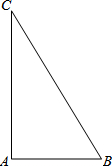 如图,△ABC是直角三角形,∠A=90°,AB=6,AC=8
如图,△ABC是直角三角形,∠A=90°,AB=6,AC=8