Question

8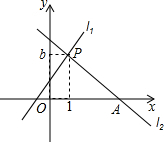．如图，直线l₁：y=x+1与直线l₂：y=mx+n交于点P（1，b），直线l₂与x轴交于点A（4，0）．
（1）求b的值；
（2）解关于x，y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$，并直接写出它的解；
（3）判断直线l₃：y=nx+m是否也经过点P？请说明理由．

Answer 1

分析 （1）由点P的坐标结合一次函数图象上点的坐标特征，即可求出b的值；
（2）利用数形结合的思想即可得出方程组的解就是两直线的交点坐标，依此即可得出结论；
（3）根据点A、P的坐标，利用待定系数法求出m、n的值，由此即可得出直线l₃的解析式，代入x=1得出y=2，由此即可得出直线l₃：y=nx+m也经过点P．

解答 解：（1）∵点P（1，b）在直线l₁：y=x+1上，
∴b=1+1=2．
（2）∵直线l₁：y=x+1与直线l₂：y=mx+n交于点P（1，2），
∴关于x，y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$．
（3）直线l₃：y=nx+m也经过点P．理由如下：
将点A（4，0）、P（1，2）代入直线l₂：y=mx+n中，
得：$\left\{\begin{array}{l}{0=4m+n}\\{2=m+n}\end{array}\right.$，解得：$\left\{\begin{array}{l}{m=-\frac{2}{3}}\\{n=\frac{8}{3}}\end{array}\right.$，
∴直线l₃：y=$\frac{8}{3}$x-$\frac{2}{3}$．
当x=1时，y=$\frac{8}{3}$×1-$\frac{2}{3}$=2，
∴直线l₃：y=$\frac{8}{3}$x-$\frac{2}{3}$经过点P（1，2）．

点评 本题考查了一次函数图象上点的坐标特征以及待定系数法求函数解析式，解题的关键是：（1）利用一次函数图象上点的坐标特征求出b值；（2）根据交点坐标得出方程组的解；（3）利用待定系数法求出m、n的值．本题属于中档题，难度不大，解决该题型题目时，根据点的坐标利用待定系数法求出函数解析式是关键．