题目内容
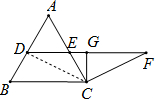
 如图,在等边△ABC中,DE∥BC交AB于点D,交AC于点E,延长DE至F点,使EF=AC,过点C作CG⊥DE于点G,求证:DG=FG.
如图,在等边△ABC中,DE∥BC交AB于点D,交AC于点E,延长DE至F点,使EF=AC,过点C作CG⊥DE于点G,求证:DG=FG.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:连接CD,易证BD=CE,∠CEF=∠ACB=60°,即可证明△BCD≌△EFC,可得CD=CF,即可证明RT△CDG≌RT△CFG,即可解题.
解答:证明:连接CD,
∵DE∥BC,
∴BD=CE,∠CEF=∠ACB=60°,
在△BCD和△EFC中,
,
∴△BCD≌△EFC(SAS),
∴CD=CF,
在RT△CDG和RT△CFG中,
,
∴RT△CDG≌RT△CFG(HL),
∴DG=FG.

∵DE∥BC,
∴BD=CE,∠CEF=∠ACB=60°,
在△BCD和△EFC中,
|
∴△BCD≌△EFC(SAS),
∴CD=CF,
在RT△CDG和RT△CFG中,
|
∴RT△CDG≌RT△CFG(HL),
∴DG=FG.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BCD≌△EFC和RT△CDG≌RT△CFG是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
若关于x的一元二次方程mx2-2x+1=0有实数根,则实数m的取值范围是( )
| A、m≥1 |
| B、m≤1 |
| C、m≥1且m≠0 |
| D、m≤1且m≠0 |
 如图,四边形ABCD的四个顶点都在⊙O上,AC是直径,DE⊥AC,垂足为点E,DE与CB的延长线相交于点F,求证:CD2=CB•CF.
如图,四边形ABCD的四个顶点都在⊙O上,AC是直径,DE⊥AC,垂足为点E,DE与CB的延长线相交于点F,求证:CD2=CB•CF.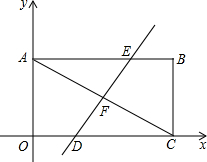 如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.
如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.