Question

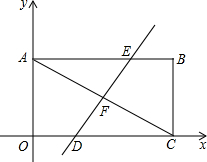如图，平面直角坐标系中，矩形OABC的对角线AC=10，边OA=6．
（1）求C点的坐标；
（2）把矩形OABC沿直线DE对折使点C落在点A处，直线DE与OC、AC、AB的交点分别为D，F，E，求折痕DE的长．

Answer 1

考点：翻折变换（折叠问题）,坐标与图形性质

专题：

分析：（1）运用勾股定理直接求出OC的长度，即可解决问题．
（2）如图，作辅助线；由题意得AD=CD=λ，则OD=8-λ；由勾股定理得：λ²=6²+（8-λ）²，求出λ的值；根据面积公式列出关于DE的方程，即可解决问题．

解答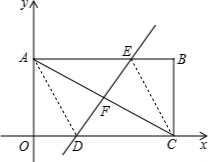：解：（1）∵四边形OABC是矩形，
∴∠AOB=90°，而OA=6，AC=10，
∴OC²=AC²-OA²=64，
∴OC=8，点C的坐标为C（8，0）．
（2）如图，连接AD、CE；
由题意得：AD=CD=λ，则OD=8-λ；
由勾股定理得：λ²=6²+（8-λ）²，
解得：λ=

25

4

；由题意知：AC⊥DE，
∴S四边形=DC•AO=

1

2

AC•DE，
∴DE=

2DC•AO

AC

=

2× 25 4 ×6

10

=

15

2

．

点评：该题主要考查了翻折变换的性质及其应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答；对综合的分析问题解决问题的能力提出了一定的要求．