题目内容
12．不等式组$\left\{\begin{array}{l}{2x-1＞0}\\{\frac{1}{3}x-1≤0}\end{array}\right.$ 的所有整数解的积为6．分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集，找出整数解，相乘可得．
解答 解：解不等式2x-1＞0，得：x＞$\frac{1}{2}$，
解不等式$\frac{1}{3}$x-1≤0，得：x≤3，
所以不等式组的解集为：$\frac{1}{2}$＜x≤3，
则该不等式组所有整数解的乘积为：1×2×3=6，
故答案为：6．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
2．在表中，我们把第i行第j列的数记为ai，j（其中i，j都是不大于3的正整数），对于表中的每个数ai，j规定如下：当i≥j时，ai，j=2i-j；当i＜j时，ai，j=i+3j．例如：当i=2，j=1时，ai，j=a2，1=3，按此规定，
（1）a1，3=10；
（2）表中这九个数的中位数是4；
（3）如果从表中这九个数中随机抽取一个数，那么抽到可能性最大的数是3；
（4）如果从表中这九个数中随机抽取一个数，那么抽到素数的概率是$\frac{2}{3}$．
（1）a1，3=10；
（2）表中这九个数的中位数是4；
（3）如果从表中这九个数中随机抽取一个数，那么抽到可能性最大的数是3；
（4）如果从表中这九个数中随机抽取一个数，那么抽到素数的概率是$\frac{2}{3}$．
| a1，1 | a1，2 | a1，3 |
| a2，1 | a2，2 | a2，3 |
| a3，1 | a3，2 | a3，3 |
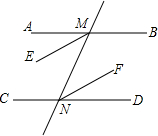如图，已知直线AB∥CD，直线MN分别交AB、CD于M、N两点，若ME、NF分别是∠AMN、∠DNM的角平分线，试说明：ME∥NF
7．下列运算正确的是（ ）
| A． | a2+a3=a5 | B． | （-a3）2=a6 | C． | 3a2•2a3=6a6 | D． | （a-b）2=a2-b2 |
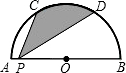如图，C、D是直径为4的半圆O上的三等分点，P是直径AB上的任意一点，连接CP、DP，则图中阴影部分的面积是$\frac{2}{3}$π．
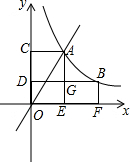如图，直线y=2x与反比例函数y=$\frac{k}{x}$（k≠0，x＞0）的图象交于点A（1，a），点B是反比例函数图象上的任意一点（不与A点重合）．
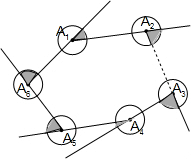如图所示，分别以n边形顶角顶点为圆心，以2cm长为半径画圆，则圆中阴影部分面积之和为4πcm2．