Question

4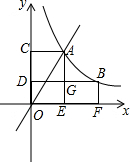．如图，直线y=2x与反比例函数y=$\frac{k}{x}$（k≠0，x＞0）的图象交于点A（1，a），点B是反比例函数图象上的任意一点（不与A点重合）．
（1）求a的值及反比例函数的解析式．
（2）过点A作AC⊥y轴，AE⊥x轴，垂足分别为C、E，过点B作BD⊥y轴，
BF⊥x轴，垂足分别为D、F，AE与BD相交于点G．设四边形ACDG和BGEF的面积分别为S₁和S₂，猜想S₁和S₂的数量关系，并说明理由．

Answer 1

分析 （1）把点A坐标代入两个函数解析式即可解决问题．
（2）由四边形ACOE与四边形DBFO面积相等即可证明．

解答 解（1）∵直线y=2x与反比例函数y=$\frac{k}{x}$（k≠0，x＞0）的图象交于点A（1，a），
∴a=2×1=2，2=$\frac{k}{1}$，
∴a=2，k=2，
∴反比例函数为y=$\frac{2}{x}$．
（2）结论：s₁=s₂．
设A（m，n），B（a，b），
∵A、B在反比例函数图象上，
∴mn=2，ab=2，
∵S_{四边形ACOE}=mn=2，S_{四边形DBFO}=ab=2，
∴S_{四边形ACOE}=S_{四边形DBFO}，
∴S_{四边形ACDG}=S_{四边形BFEG}，
即s₁=s₂．

点评 本题考查一次函数与反比例函数的交点问题，学会待定系数法确定函数解析式，理解反比例函数中比例系数K的几何意义，属于中考常考题型．