题目内容
17.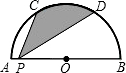 如图,C、D是直径为4的半圆O上的三等分点,P是直径AB上的任意一点,连接CP、DP,则图中阴影部分的面积是$\frac{2}{3}$π.
如图,C、D是直径为4的半圆O上的三等分点,P是直径AB上的任意一点,连接CP、DP,则图中阴影部分的面积是$\frac{2}{3}$π.
分析 连接OC、OD、CD,利用同底等高的三角形面积相等可知阴影部分的面积等于扇形OCD的面积,然后计算扇形面积就可.
解答  解:连接OC、OD、CD.
解:连接OC、OD、CD.
∵△COD和△CDA等底等高,
∴S△COD=S△ACD.
∵点C,D为半圆的三等分点,
∴∠COD=180°÷3=60°,
∴阴影部分的面积=S扇形COD=$\frac{60π•{2}^{2}}{360}$=$\frac{2}{3}$π.
故答案为:$\frac{2}{3}$π.
点评 此题主要考查了扇形面积求法,利用已知得出理解阴影部分的面积等于扇形OCD的面积是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.公园路中学组织了一次教师踢毽子比赛,甲、乙两教研组每队各10人的比赛成绩如表(10分制):
(1)甲队成绩的中位数是9.5分,乙队成绩的众数是10 分.
(2)计算乙队的平均成绩和方差.
(3)已知甲队的成绩的方差是1.4,则成绩较为整齐的是乙 队.
| 甲 | 7 | 9 | 8 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 7 | 8 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)计算乙队的平均成绩和方差.
(3)已知甲队的成绩的方差是1.4,则成绩较为整齐的是乙 队.
6.二十一世纪,纳米技术将被广泛应用,纳米是长度计量单位,1纳米=0.000000001米,则5纳米可以用科学记数法表示为( )
| A. | 5×109米 | B. | 50×10-8米 | C. | 5×10-9米 | D. | 5×10-8米 |
