题目内容
1.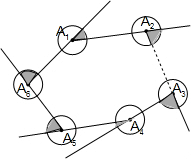 如图所示,分别以n边形顶角顶点为圆心,以2cm长为半径画圆,则圆中阴影部分面积之和为4πcm2.
如图所示,分别以n边形顶角顶点为圆心,以2cm长为半径画圆,则圆中阴影部分面积之和为4πcm2.
分析 由于多边形的外角和为360°,则所有阴影的扇形的圆心角的和为360度,故阴影部分的面积=π×22=4π.
解答 解:∵多边形的外角和为360°,
∴SA1+SA2+…+SAn=S圆=π×22=π(cm2).
故答案为4π.
点评 本题考查了圆的面积公式的应用,多边形的外角和定理,扇形的面积计算,关键是正确找出阴影部分面积的计算方法.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
6.二十一世纪,纳米技术将被广泛应用,纳米是长度计量单位,1纳米=0.000000001米,则5纳米可以用科学记数法表示为( )
| A. | 5×109米 | B. | 50×10-8米 | C. | 5×10-9米 | D. | 5×10-8米 |
10.下列说法正确的个数是( )
①两条直线被第三条直线所截,则同旁内角一定互补;
②若线段a、b、c,满足b+c>a,则以a、b、c为边一定能组成三角形;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分;
⑤△ABC在平移过程中,对应线段一定相等.
①两条直线被第三条直线所截,则同旁内角一定互补;
②若线段a、b、c,满足b+c>a,则以a、b、c为边一定能组成三角形;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分;
⑤△ABC在平移过程中,对应线段一定相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.若x2+3x-5的值为7,则3x2+9x-2的值为( )
| A. | 5 | B. | 16 | C. | 21 | D. | 34 |
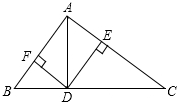 如图,在Rt△ABC中,AB⊥AC,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E,F,则图中与∠C(∠C除外)相等的角的个数是( )
如图,在Rt△ABC中,AB⊥AC,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E,F,则图中与∠C(∠C除外)相等的角的个数是( ) 如图,AD∥BC,∠A=104°,∠D=126°,BE、CE分别是∠ABC和∠BCD的角平分线,则∠BEC的度数为115°.
如图,AD∥BC,∠A=104°,∠D=126°,BE、CE分别是∠ABC和∠BCD的角平分线,则∠BEC的度数为115°.