题目内容
2.在表中,我们把第i行第j列的数记为ai,j(其中i,j都是不大于3的正整数),对于表中的每个数ai,j规定如下:当i≥j时,ai,j=2i-j;当i<j时,ai,j=i+3j.例如:当i=2,j=1时,ai,j=a2,1=3,按此规定,(1)a1,3=10;
(2)表中这九个数的中位数是4;
(3)如果从表中这九个数中随机抽取一个数,那么抽到可能性最大的数是3;
(4)如果从表中这九个数中随机抽取一个数,那么抽到素数的概率是$\frac{2}{3}$.
| a1,1 | a1,2 | a1,3 |
| a2,1 | a2,2 | a2,3 |
| a3,1 | a3,2 | a3,3 |
分析 (1)根据对于表中的每个数ai,j规定如下:当i≥j时,ai,j=2i-j;当i<j时,ai,j=i+3j.可得a1,3的值;
(2)分别求出表中这九个数的值,再根据中位数的定义求解;
(3)抽到可能性最大的数即九个数中出现频数最多的数,概率最大的数,根据概率公式求解即可;
(4)用这九个数中素数的个数除以9即可.
解答 解:(1)a1,3=1+3×3=10;
(2)∵a1,1=2×1-1=1,a1,2=1+3×2=7,a1,3=10,
a2,1=2×2-1=3,a2,2=2×2-2=2,a2,3=2+3×3=11,
a3,1=2×3-1=5,a3,2=2×3-2=4,a3,3=2×3-3=3,
∴这九个数按从小到大排列为:1,2,3,3,4,5,7,10,11,
∴表中这九个数的中位数是4;
(3)∵这九个数为:1,2,3,3,4,5,7,10,11,
∴如果从表中这九个数中随机抽取一个数,那么抽到可能性最大的数是3;
(4)∵这九个数中素数有2,3,3,5,7,11,一共6个,
∴如果从表中这九个数中随机抽取一个数,那么抽到素数的概率是$\frac{6}{9}$=$\frac{2}{3}$.
故答案为10;4;3;$\frac{2}{3}$.
点评 本题考查了概率公式:概率=所求情况数与总情况数之比.也考查了中位数的定义,可能性的大小,根据题目规定求出表中九个数的值是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
3.如果x2-px+q=(x+a)(x+b),那么p等于( )
| A. | ab | B. | a+b | C. | -ab | D. | -(a+b) |
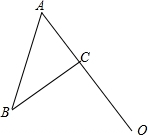 如图,在△ABC中,AB=5,BC=4,AC=3,点O在AC的延长线上,且OC=4.
如图,在△ABC中,AB=5,BC=4,AC=3,点O在AC的延长线上,且OC=4.
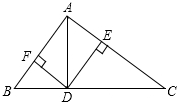 如图,在Rt△ABC中,AB⊥AC,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E,F,则图中与∠C(∠C除外)相等的角的个数是( )
如图,在Rt△ABC中,AB⊥AC,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E,F,则图中与∠C(∠C除外)相等的角的个数是( )