题目内容
3.完成下列问题:(1)若n(n≠0)是关于x的方程x2+mx+2n=0的根,求m+n的值;
(2)已知x,y为实数,且y=$\sqrt{2x-5}$$+\sqrt{5-2x}$-3,求2xy的值.
分析 (1)利用方程解的定义找到相等关系n2+mn+2n=0,再把所求的代数式化简后整理出m+n=-2,即为所求;
(2)根据被开方数大于等于0列式求出x,再求出y,然后代入代数式进行计算即可得解.
解答 解:(1)由题意得n2+mn+2n=0,∵n≠0,
∴n+m+2=0,
得m+n=-2;
(2)解:由题意得,2x-5≥0且5-2x≥0,
解得x≥$\frac{5}{2}$且x≤$\frac{5}{2}$,
所以,$x=\frac{5}{2}$,y=-3,
∴2xy=-15.
点评 考查了一元二次方程的解及二次根式有意义的条件,解题的关键是能够了解方程的解的定义,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.如果x2-px+q=(x+a)(x+b),那么p等于( )
| A. | ab | B. | a+b | C. | -ab | D. | -(a+b) |
18.方程$\sqrt{x+1}$=5-x的解是( )
| A. | x=3 | B. | x=8 | C. | x1=3,x2=8 | D. | x1=3,x2=-8 |
15.把线段AB沿水平方向平移5cm,平移后的像为线段CD,则线段AB与线段CD之间的距离是( )
| A. | 等于5cm | B. | 小于5cm | C. | 小于或等于5cm | D. | 大于或等于5cm |
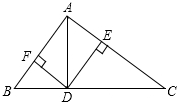 如图,在Rt△ABC中,AB⊥AC,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E,F,则图中与∠C(∠C除外)相等的角的个数是( )
如图,在Rt△ABC中,AB⊥AC,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E,F,则图中与∠C(∠C除外)相等的角的个数是( ) 如图,AD∥BC,∠A=104°,∠D=126°,BE、CE分别是∠ABC和∠BCD的角平分线,则∠BEC的度数为115°.
如图,AD∥BC,∠A=104°,∠D=126°,BE、CE分别是∠ABC和∠BCD的角平分线,则∠BEC的度数为115°.