题目内容
20.在平面直角坐标系中,有三条直线l1,l2,l3,它们的函数解析式分别是y=x,y=x+1,y=x+2.在这三条直线上各有一个动点,依次为A,B,C,它们的横坐标分别为a,b,c,则当a,b,c满足条件a=b=c或a=b+1=c+2或$\frac{a-c}{a-b}$=2时,这三点不能构成△ABC.分析 若不能构成三角形,就是这三个动点在一条直线上的时候,在一条直线有三种情况,(1)动点的横坐标相等;(2)动点的纵坐标相等;(3)三点满足一次函数式.
解答 解:(1)动点的横坐标相等时:a=b=c.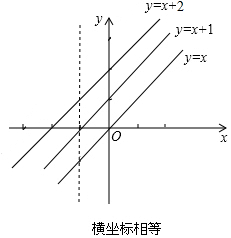
(2)动点的纵坐标相等时:∵y=a,y=b+1,y=c+2,
∴a=b+1=c+2.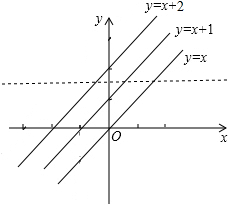
(3)三点满足一次函数式,三点可以表示一次函数的斜率:斜率为函数图象与x轴所形成角的正切值;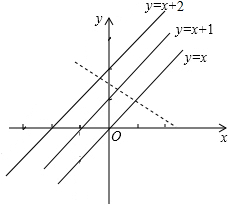
∵三点的坐标为(a,a),(b,b+1),(c,c+2),
∴$\frac{b+1-a}{b-a}$=$\frac{c+2-a}{c-a}$,
1+$\frac{1}{b-a}$=1+$\frac{2}{c-a}$,
∴$\frac{a-c}{a-b}$=2.
故答案为:a=b=c或a=b+1=c+2或$\frac{a-c}{a-b}$=2.
点评 本题考查两条直线相交或平行问题,关键是知道动点满足什么条件时不能构成三角形,即动点在同一直线上时不能三角形,从而可求解.

练习册系列答案
相关题目
11.下列判断中,你认为正确的是( )
| A. | 0的倒数是0 | B. | π是有理数 | C. | $\sqrt{5}$大于2 | D. | $\sqrt{9}$的值是±3 |
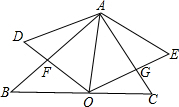 如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.
如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.