题目内容
4.已知一次函数y=2x与y=-x+b的交点为(1,a),则方程组$\left\{\begin{array}{l}2x-y=0\\ x+y-b=0\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.分析 先把(1,a)代入y=2x可确定交点坐标,然后根据方程组的解就是两个相应的一次函数图象的交点坐标求解.
解答 解:把(1,a)代入y=2x得a=2,
所以方程组$\left\{\begin{array}{l}2x-y=0\\ x+y-b=0\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
故答案为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
点评 本题考查了一次函数与二元一次方程(组):方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
14.在数轴上与原点的距离小于5的点对应的x满足( )
| A. | -5<x<5 | B. | x<5 | C. | x<-5或x>5 | D. | x>5 |
13.下列说法正确的是( )
| A. | 平角是一条直线 | B. | 角的边越长,角越大 | ||
| C. | 大于直角的角叫做钝角 | D. | 两个锐角的和不一定是钝角 |
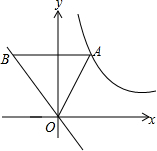 如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.
如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.