题目内容
17. 如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
分析 连结OM、OP,作OH⊥AB于H,如图,先利用坐标轴上点的坐标特征求出A点和B点坐标,则可判断△OAB为等腰直角三角形,从而得到OH=$\frac{1}{2}$AB=2,再根据切线的性质得OM⊥PM,利用勾股定理得到PM=$\sqrt{O{P}^{2}-1}$,则可判断OP的长最小时,PM的长最小,然后利用垂线段最短得到OP的最小值,再计算PM的最小值.
解答 解:连结OM、OP,作OH⊥AB于H,如图,
当x=0时,y=-x+2$\sqrt{2}$=2$\sqrt{2}$,则A(0,2$\sqrt{2}$),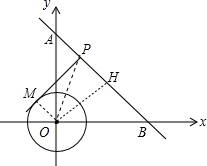
当y=0时,-x+2$\sqrt{2}$=0,解得x=2$\sqrt{2}$,则B(2$\sqrt{2}$,0),
所以△OAB为等腰直角三角形,则AB=$\sqrt{2}$OA=4,OH=$\frac{1}{2}$AB=2,
因为PM为切线,
所以OM⊥PM,
所以PM=$\sqrt{O{P}^{2}-O{M}^{2}}$=$\sqrt{O{P}^{2}-1}$,
当OP的长最小时,PM的长最小,而OP=OH=2时,OP的长最小,
所以PM的最小值为$\sqrt{{2}^{2}-1}$=$\sqrt{3}$.
故选D.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.解决本题的关键是用OP、OM表示PM,利用OP的最小值计算PM的最小值.

练习册系列答案
相关题目
12.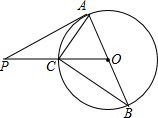 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )| A. | 3$\sqrt{3}$ | B. | 4 | C. | 5 | D. | 6 |
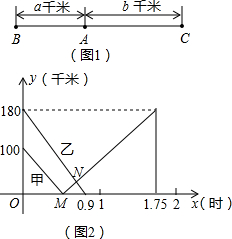 金温高铁于2015年12月26日正式开通,且被誉为“浙江最美高铁”的线路.如图1所示,已知金温高铁上有A,B,C三站,B,C两站相距280千米,甲、乙两列动车分别从B,C两站同时沿铁路匀速相向出发向终点站C,B而行,甲、乙两动车离A站的距离y(千米)与行驶时间x(时)的关系如图2所示,很据图象,解答以下问题:
金温高铁于2015年12月26日正式开通,且被誉为“浙江最美高铁”的线路.如图1所示,已知金温高铁上有A,B,C三站,B,C两站相距280千米,甲、乙两列动车分别从B,C两站同时沿铁路匀速相向出发向终点站C,B而行,甲、乙两动车离A站的距离y(千米)与行驶时间x(时)的关系如图2所示,很据图象,解答以下问题: 如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于60°或120°.
如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于60°或120°.