题目内容
12.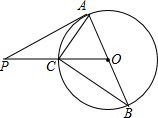 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )| A. | 3$\sqrt{3}$ | B. | 4 | C. | 5 | D. | 6 |
分析 先证明△OAC为等边三角形得到∠AOC=60°,再根据切线的性质得到∠OAP=90°,然后根据正切的定义计算PA的长.
解答 解:∵OB=OC,
∴∠B=∠BCO,
∴∠AOC=∠B+∠BCO,
∴∠AOC=2∠BCO,
而∠BAC=2∠BCO,
∴∠BAC=∠AOC,
∴CA=CO,
而OA=OC,
∴OA=OC=AC=3,
∴△OAC为等边三角形,
∴∠AOC=60°,
∵PA切⊙O于点A,
∴OA⊥PA,
∴∠OAP=90°,
∵tan∠AOB=$\frac{PA}{OA}$,
∴PA=3tan60°=3$\sqrt{3}$.
故选A.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.解决本题的关键是证明△AOC为等边三角形.

练习册系列答案
相关题目
2.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (ab)2=ab2 | C. | 2a4×3a5=6a9 | D. | (a2)3=a5 |
3.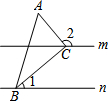 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )
 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
20.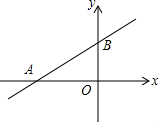 如图,直线y=$\frac{3}{4}x+3$与x、y轴分别交于A、B两点,则cos∠BAO的值是( )
如图,直线y=$\frac{3}{4}x+3$与x、y轴分别交于A、B两点,则cos∠BAO的值是( )
 如图,直线y=$\frac{3}{4}x+3$与x、y轴分别交于A、B两点,则cos∠BAO的值是( )
如图,直线y=$\frac{3}{4}x+3$与x、y轴分别交于A、B两点,则cos∠BAO的值是( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
17. 如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
 如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
2.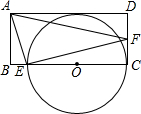 如图,矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,以EC为直径的⊙O与AD相切,则tan∠AFE的值为( )
如图,矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,以EC为直径的⊙O与AD相切,则tan∠AFE的值为( )
 如图,矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,以EC为直径的⊙O与AD相切,则tan∠AFE的值为( )
如图,矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,以EC为直径的⊙O与AD相切,则tan∠AFE的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
 如图,AB∥DE,△ACB是等腰直角三角形,且∠C=90°,CB的延长线交DE于点G,则∠CGE=135度.
如图,AB∥DE,△ACB是等腰直角三角形,且∠C=90°,CB的延长线交DE于点G,则∠CGE=135度.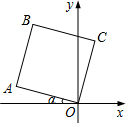 将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为(-$\sqrt{2}$,$\sqrt{6}$).
将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为(-$\sqrt{2}$,$\sqrt{6}$).