题目内容
12. 如图,正三角形ABC中,在AB,AC边上分别取点M,N使BM=AN,连BN,CM,求证:
如图,正三角形ABC中,在AB,AC边上分别取点M,N使BM=AN,连BN,CM,求证:(1)BN=CM;
(2)∠NOC=60°.
分析 (1)由正三角形的性质得出∠A=∠ABC=60°,AB=BC,由SAS证明△ABN≌△BCM,得出对应边相等即可;
(2)由全等三角形的性质得出∠ABN=∠BCM,得出∠NOC=∠BCM+∠OBC=∠ABN+∠OBC=60°即可.
解答 证明:(1)∵△ABC是正三角形,
∴∠A=∠ABC=60°,AB=BC,
在△ABN和△BCM中,$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠A=∠ABC}&{\;}\\{AN=BM}&{\;}\end{array}\right.$,
∴△ABN≌△BCM(SAS),
∴BN=CM;
(2)由(1)得:△ABN≌△BCM,
∴∠ABN=∠BCM,
又∵∠ABN+∠OBC=60°,
∴∠BCM+∠OBC=60°,
∴∠NOC=60°.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质,三角形的外角性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
19.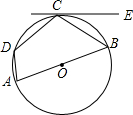 如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
 如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )| A. | 145° | B. | 125° | C. | 90° | D. | 80° |
2.下列结论成立的是( )
| A. | 若|a|=a,则a>0 | B. | 若|a|=|b|,则a=±b | C. | 若|a|>a,则a≤0 | D. | 若|a|>|b|,则a>b. |
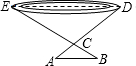 如图,为了测量一池塘的宽DE,在岸边找一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE,交EC的延长线于B,测得AB=6m,求池塘的宽DE.
如图,为了测量一池塘的宽DE,在岸边找一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE,交EC的延长线于B,测得AB=6m,求池塘的宽DE.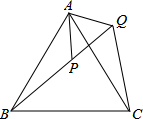 等边△ABC、等边△APQ中,点P在△ABC内,点Q在△ABC外,求证:BP=CQ.
等边△ABC、等边△APQ中,点P在△ABC内,点Q在△ABC外,求证:BP=CQ. 如图.已知点B、C、D在同一条直线上.△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,
如图.已知点B、C、D在同一条直线上.△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,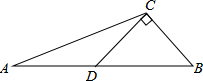 如图,CD是△ABC的中线,CD⊥CB,∠ACD=30°,求证:AC=2BC.
如图,CD是△ABC的中线,CD⊥CB,∠ACD=30°,求证:AC=2BC.